题目内容
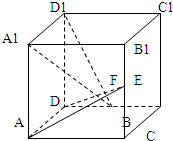 如果正方体ABCD-A1B1C1D1中EF分别是BB1、CD中点.
如果正方体ABCD-A1B1C1D1中EF分别是BB1、CD中点.(1)求证:AD⊥D1F;
(2)求证:平面AED⊥平面A1FD1;
(3)若AB=2,求VE-AA1F.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的性质,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)通过证明AD⊥平面CDD1C1,然后利用直线与平面垂直的性质定理证明AD⊥D1F;
(2)通过证明D1F⊥平面ADE,然后利用平面与平面垂直的判定定理证明平面AED⊥平面A1FD1;
(3)利用AB=2,通过等体积求解,求出底面面积,即可求VE-AA1F.
(2)通过证明D1F⊥平面ADE,然后利用平面与平面垂直的判定定理证明平面AED⊥平面A1FD1;
(3)利用AB=2,通过等体积求解,求出底面面积,即可求VE-AA1F.
解答:
(1)证明:由正方体ABCD-A1B1C1D1⇒AD⊥DD1,AD⊥DC,DD1∩DC=D,∴AD⊥平面CDD1C1,
∵D1F?平面CDD1C1,∴AD⊥D1F;
(2)证明:在AB上取中点F1,则A1F1∥D1F,又在正方形ABB1A1中可证AE⊥A1F1,⇒AE⊥D1F,
又∵AD⊥D1F,AE∩AD=A,∴D1F⊥平面ADE,D1F?平面A1FD1
∴平面AED⊥平面A1FD1;
(3)解:∵S△AA1E=S△AA1B=2,
∴VF-AA1E=VF-AA1B=
•2•2=
.
∵D1F?平面CDD1C1,∴AD⊥D1F;
(2)证明:在AB上取中点F1,则A1F1∥D1F,又在正方形ABB1A1中可证AE⊥A1F1,⇒AE⊥D1F,
又∵AD⊥D1F,AE∩AD=A,∴D1F⊥平面ADE,D1F?平面A1FD1
∴平面AED⊥平面A1FD1;
(3)解:∵S△AA1E=S△AA1B=2,
∴VF-AA1E=VF-AA1B=
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题考查几何体的体积的求法,直线与平面垂直,平面与平面垂直的判定定理以及性质定理的应用,考查空间想象能力,逻辑推理能力.转化思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知命题P:?x∈(-∞,0),2x<3x;命题q:?a>0函数f(x)=ln2x+lnx-a有零点.则下列命题为真命题的是( D )( )
| A、p∧q |
| B、p∨(¬q) |
| C、p∧(¬q) |
| D、(¬p)∧q |
已知向量
=(2,1),
=(1,x),若
⊥
,则实数x的值为( )
| a |
| b |
| a |
| b |
| A、-2 | B、-1 | C、0 | D、1 |
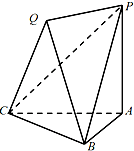 在空间几何体PQ-ABC中,PA⊥平面ABC,平面QBC⊥平面ABC,AB=AC,QB=QC.
在空间几何体PQ-ABC中,PA⊥平面ABC,平面QBC⊥平面ABC,AB=AC,QB=QC.