题目内容
已知等差数列{an}满足:
=a5
+a19
,且A、B、C三点共线(该直线不过O点),则a3+a13+a20=( )
| OA |
| OB |
| OC |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:首先,根据A、B、C三点共线(该直线不过O点),得到a5+a19=1,然后,结合等差数列的基本性质求解.
解答:
解:∵A、B、C三点共线(该直线不过O点),
∴a5+a19=1,
∴2a12=1,
∵a3+a13+a20
=a4+a12+a20
=3a12=
,
∴a3+a13+a20=
,
故选:A.
∴a5+a19=1,
∴2a12=1,
∵a3+a13+a20
=a4+a12+a20
=3a12=
| 3 |
| 2 |
∴a3+a13+a20=
| 3 |
| 2 |
故选:A.
点评:本题重点考查了三点共线的条件、等差数列的基本性质等知识,属于中档题.

练习册系列答案
相关题目
函数f(x)=sinx,x∈R的最小正周期是( )
| A、π | ||
| B、2π | ||
| C、4π | ||
D、
|
若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为( )
| A、27π | B、9π | C、3π | D、π |
已知向量
=(2,1),
=(1,x),若
⊥
,则实数x的值为( )
| a |
| b |
| a |
| b |
| A、-2 | B、-1 | C、0 | D、1 |
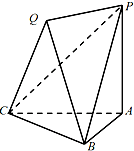 在空间几何体PQ-ABC中,PA⊥平面ABC,平面QBC⊥平面ABC,AB=AC,QB=QC.
在空间几何体PQ-ABC中,PA⊥平面ABC,平面QBC⊥平面ABC,AB=AC,QB=QC.