题目内容

组成一个由10人组成的球队，他们由七个学校组成，每校至少有一人，其各部分配方案共有
 
种．
考点：排列、组合及简单计数问题
专题：应用题,排列组合
分析：由题意知十个报送名额之间没有区别，可将原问题转化为10个元素之间有9个间隔，要求分成7份，每份不空，使用插空法，相当于用6块档板插在101个间隔中，计算可得答案．
解答： 解：根据题意，将10个名额，分配给7所学校，每校至少有1个名额，
可以转化为10个元素之间有9个间隔，要求分成7份，每份不空；
相当于用6块档板插在9个间隔中，共有
C
6
9
=84种不同方法．
故答案为：84．
点评：本题考查排列、组合的综合运用，要求学生会一些特殊方法的使用，如插空法、隔板法等；但首先应该会把实际问题转化为对应问题的模型．
练习册系列答案
相关题目
如图是函数f（x）=Asin（ωx+φ）（A＞0，0＜ω＜3，0＜φ＜π）的图象的一部分，则ωφ=（　　）
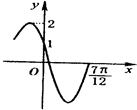
A、
π
3
B、
5π
3
C、
5π
12
D、
5π
6
已知a＞0，b＞0，
1
a
+
1
b
=1，则a+b+
a2+b2
的最小值是
 
．
在棱长为1的正方体ABCD-A1B1C1D1中．
（1）求证：AC⊥平面B1 BDD1
（2）求二面角A-B1D1-A1的正切值．
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）右焦点F，右准线与一条渐近线交于点A，△OAF的面积为
3
6
a2 （O为坐标原点），则双曲线的两条渐近线的夹角为
 
．
11名工人中，有5人只能当钳工，4人只能当车工，另外2人既能当钳工又能当车工．先从11人中选出4人当钳工，4人当车工，问有多少种不同的选法？
在空间直角坐标系中，对其中任何一向量X=（x1，x2，x3），定义范数||X||，它满足以下性质：
（1）||X||≥0，当且仅当X为零向量时，不等式取等号；
（2）对任意的实数λ，||λX||=|λ|•||X||（注：此处点乘号为普通的乘号）；
（3）||X||+||Y||≥||X+Y||．在平面直角坐标系中，有向量X=（x1，x2），
下面给出的几个表达式中，可能表示向量X的范数的是
 
（把所有正确答案的序号都填上）
（1）
x
2
1
+2
x
2
2
       （2）
2
x
2
1
-
x
2
2
     （3）
x
2
1
+
x
2
2
+2
       （4）
x
2
1
+
x
2
2
．
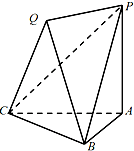在空间几何体PQ-ABC中，PA⊥平面ABC，平面QBC⊥平面ABC，AB=AC，QB=QC．
（1）求证：PA∥平面QBC；
（2）若PQ⊥平面QBC，试比较三棱锥Q-PBC与P-ABC的体积的大小，并说明理由．
设函数f（x）=x3+ax2-a2x-1，二次函数g（x）=ax2-x-1
（1）若a＜0，求f（x）的单调区间；
（2）当函数y=f（x）与y=g（x）的图象只有一个公共点且g（x）存在最大值时，记g（x）的最大值为h（a），求函数h（a）的解析式；
（3）若函数f（x）与g（x）在区间（a-2，a）内均为增函数，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网