题目内容
MCD⊥平面BCD,AB⊥平面BCD,AB=2
.
(1)求点A到平面MBC的距离;
(2)求平面ACM与平面BCD所成二面角的正弦值.
| 3 |
(1)求点A到平面MBC的距离;
(2)求平面ACM与平面BCD所成二面角的正弦值.
考点:用空间向量求平面间的夹角,点、线、面间的距离计算,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:取CD中点O,连OB,OM,以O为原点,直线OC、BO、OM为x轴,y轴,z轴,建立空间直角坐标系,求出O,C,M,B,A的坐标
(1)求出平面MBC的法向量,利用空间距离公式求解即可.
(2)求出设平面ACM的法向量,平面BCD的法向量,利用空间向量的数量积求解即可.
(1)求出平面MBC的法向量,利用空间距离公式求解即可.
(2)求出设平面ACM的法向量,平面BCD的法向量,利用空间向量的数量积求解即可.
解答:
解:取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,又平面MCD⊥平面BCD,则MO⊥平面BCD.
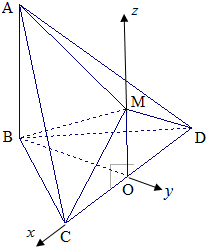
以O为原点,直线OC、BO、OM为x轴,y轴,z轴,建立空间直角坐标系如图.
OB=OM=
,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,
),B(0,-
,0),A(0,-
,2
),
(1)设
=(x,y,z)是平面MBC的法向量,则
=(1,
,0),
=(0,
,
),由
⊥
得x+
y=0;由
⊥
得
y+
z=0;取
=(
,-1,1),
=(0,0,2
),则距离d=
=
(2)
=(-1,0,
),
=(-1,-
,2
).
z设平面ACM的法向量为
=(x,y,z),
由
得
.解得x=
z,y=z,取
=(
,1,1).
又平面BCD的法向量为
=(0,0,1),则cos<
,
>=
=
设所求二面角为θ,则sinθ=
=
.

以O为原点,直线OC、BO、OM为x轴,y轴,z轴,建立空间直角坐标系如图.
OB=OM=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
(1)设
| n |
| BC |
| 3 |
| BM |
| 3 |
| 3 |
| n |
| BC |
| 3 |
| n |
| BM |
| 3 |
| 3 |
| n |
| 3 |
| BA |
| 3 |
|
| ||||
|
|
2
| ||
| 5 |
(2)
| CM |
| 3 |
| CA |
| 3 |
| 3 |
z设平面ACM的法向量为
| n1 |
由
|
|
| 3 |
| n1 |
| 3 |
又平面BCD的法向量为
| n |
| n1 |
| n |
| ||||
|
|
| 1 | ||
|
设所求二面角为θ,则sinθ=
1-(
|
2
| ||
| 5 |
点评:本题考查空间向量的应用,点到平面的距离的解法,二面角的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为( )
| A、27π | B、9π | C、3π | D、π |
由
>
,
>
,
>
若a>b>0,m>0,则
与
的关系( )
| 7 |
| 10 |
| 5 |
| 8 |
| 9 |
| 11 |
| 8 |
| 10 |
| 21 |
| 25 |
| 15 |
| 19 |
| b+m |
| a+m |
| b |
| a |
| A、相等 | B、前者大 |
| C、后者大 | D、不确定 |
