题目内容
圆锥的母线长为6,轴截面的顶角为120度,过两条母线作截面,则截面面积的最大值为( )
A、9
| ||
| B、18 | ||
C、18
| ||
| D、9 |
考点:旋转体(圆柱、圆锥、圆台),棱锥的结构特征
专题:空间位置关系与距离
分析:作出过圆锥顶点的截面,两条母线的夹角是90°时,截面三角形的最大面积,结合母线长为6,代入可得截面面积的最大值.
解答:
 解:如图,过圆锥顶点P认作一截面PAB,交底面圆与AB,
解:如图,过圆锥顶点P认作一截面PAB,交底面圆与AB,
∵圆锥轴截面的顶角为120°,
则∠APB=90°,截面面积取最大值,
∴过圆锥顶点的截面中,最大截面面积为
l2=18,
故选:B
 解:如图,过圆锥顶点P认作一截面PAB,交底面圆与AB,
解:如图,过圆锥顶点P认作一截面PAB,交底面圆与AB,∵圆锥轴截面的顶角为120°,
则∠APB=90°,截面面积取最大值,
∴过圆锥顶点的截面中,最大截面面积为
| 1 |
| 2 |
故选:B
点评:本题考查了圆锥的结构特征,学生解答此题时容易出错,往往不假思索的认为截面积最大的是轴截面,该题是否是轴截面面积最大取决于轴截面的顶角,此题是基础题.

练习册系列答案
相关题目
函数f(x)=sinx,x∈R的最小正周期是( )
| A、π | ||
| B、2π | ||
| C、4π | ||
D、
|
已知命题P:?x∈(-∞,0),2x<3x;命题q:?a>0函数f(x)=ln2x+lnx-a有零点.则下列命题为真命题的是( D )( )
| A、p∧q |
| B、p∨(¬q) |
| C、p∧(¬q) |
| D、(¬p)∧q |
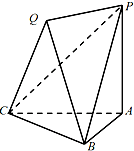 在空间几何体PQ-ABC中,PA⊥平面ABC,平面QBC⊥平面ABC,AB=AC,QB=QC.
在空间几何体PQ-ABC中,PA⊥平面ABC,平面QBC⊥平面ABC,AB=AC,QB=QC.