题目内容
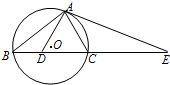已知圆O的内接△ABC中，D为BC上一点，且△ADC为正三角形，点E为BC的延长线上一点，AE为圆O的切线，求证：CD2=BD•EC．考点：与圆有关的比例线段
专题：选作题,立体几何
分析：先证明△ABD∽△EAC，可得AD•CA=BD•EC，再结合△ACD为等边三角形，所以AD=AC=CD，即可得出结论．
解答：
证明：因为AE为圆O的切线，所以∠ABD=∠CAE． …（2分）
因为△ACD为等边三角形，所以∠ADC=∠ACD，
所以∠ADB=∠ECA，所以△ABD∽△EAC． …（6分）
所以
=
，即AD•CA=BD•EC． …（8分）
因为△ACD为等边三角形，所以AD=AC=CD，
所以CD2=BD•EC．…（10分）
因为△ACD为等边三角形，所以∠ADC=∠ACD，
所以∠ADB=∠ECA，所以△ABD∽△EAC． …（6分）
所以
| AD |
| BD |
| EC |
| CA |
因为△ACD为等边三角形，所以AD=AC=CD，
所以CD2=BD•EC．…（10分）
点评：本题考查三角形相似的判断，考查圆的切线的性质，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
如图，在△ABC中，AD是的∠A的平分线，圆O经过点A与BC切于点D，与AB，AC相交于E、F，连结DF，DE．