题目内容
已知复数z=lg（m2-2m-2）+（m2+3m+2）i．
（1）当z为纯虚数时，求实数m的值；
（2）当z为实数时，求实数m的值；
（3）当复数z在复平面内对应的点位于第二象限时，求实数的取值范围．
（1）当z为纯虚数时，求实数m的值；
（2）当z为实数时，求实数m的值；
（3）当复数z在复平面内对应的点位于第二象限时，求实数的取值范围．
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：（1）当z为纯虚数时，
，解得即可；
（2）当z为实数时，
，解得即可；
（3）当复数z在复平面内对应的点位于第二象限时，
，解得即可．
|
（2）当z为实数时，
|
（3）当复数z在复平面内对应的点位于第二象限时，
|
解答：
解：（1）当z为纯虚数时，
，解得m=3；
（2）当z为实数时，
，解得m=-1或m=-2；
（3）当复数z在复平面内对应的点位于第二象限时，
，
由0＜m2-2m-2＜1，解得1+
＜m＜3或-1＜m＜1-
．
由m2+3m+2＞0解得m＞-1或m＜-2．
∴解得-1＜m＜1-
或1+
＜m＜3．
∴实数的取值范围是(-1，1-
)∪(1+
，3)．
|
（2）当z为实数时，
|
（3）当复数z在复平面内对应的点位于第二象限时，
|
由0＜m2-2m-2＜1，解得1+
| 3 |
| 3 |
由m2+3m+2＞0解得m＞-1或m＜-2．
∴解得-1＜m＜1-
| 3 |
| 3 |
∴实数的取值范围是(-1，1-
| 3 |
| 3 |
点评：本题考查了复数为实数、纯虚数的充要条件和几何意义，属于中档题．
练习册系列答案
相关题目
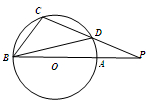如图，AB是半径为3的⊙O的直径，CD是弦，BA，CD的延长线交于点P，PA=4，PD=5，则∠CBD=
如图，在△ABC中，AD是的∠A的平分线，圆O经过点A与BC切于点D，与AB，AC相交于E、F，连结DF，DE．