题目内容
在大街上，随机调查339名成人，有关吸烟、不吸烟、患支气管炎、不患支气管炎的数据如下表所示．
根据表中数据：
（1）判断：吸烟与患支气管炎是否有关？
（2）用假设检验的思想予以证明．
| 患支气管炎 | 为患支气管炎 | 总计 | |
| 吸烟 | 43 | 162 | 205 |
| 不吸烟 | 13 | 121 | 134 |
| 总计 | 56 | 283 | 339 |
（1）判断：吸烟与患支气管炎是否有关？
（2）用假设检验的思想予以证明．
考点：独立性检验的应用
专题：计算题,概率与统计
分析：（1）根据列联表所给的数据，代入求观测值的公式，求出观测值，把观测值同临界值进行比较，可得结论；
（2）假设吸烟与患支气管炎无关，可得小概率事件发生了，进而假设错误，得到吸烟与患支气管炎有关．
（2）假设吸烟与患支气管炎无关，可得小概率事件发生了，进而假设错误，得到吸烟与患支气管炎有关．
解答：
解：（1）由列联表中的数据，得K2=
=7.469＞6.635
所以，有99%的把握认为吸烟与患支气管炎有关．
（2）假设吸烟与患支气管炎无关，由于A=P（K2＞6.635）≈0.01，即A为小概率事件，而小概率事件发生了，进而假设错误，得到吸烟与患支气管炎有关．
| 339×(13×162-43×121)2 |
| 205×134×56×283 |
所以，有99%的把握认为吸烟与患支气管炎有关．
（2）假设吸烟与患支气管炎无关，由于A=P（K2＞6.635）≈0.01，即A为小概率事件，而小概率事件发生了，进而假设错误，得到吸烟与患支气管炎有关．
点评：本题考查独立性检验的应用解题的关键是正确利用观测值公式求出观测值，正确理解临界值对应的概率的意义．
练习册系列答案
小学教材完全解读系列答案
相关题目
i是虚数单位，复数z=i-1，则|z|=（ ）
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
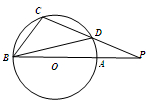如图，AB是半径为3的⊙O的直径，CD是弦，BA，CD的延长线交于点P，PA=4，PD=5，则∠CBD=
如图，在△ABC中，AD是的∠A的平分线，圆O经过点A与BC切于点D，与AB，AC相交于E、F，连结DF，DE．