题目内容
已知sinβ=
(
<β<π),且sin(α+β)=cosα,则tan(α+β)= .
| 3 |
| 5 |
| π |
| 2 |
考点:两角和与差的正弦函数,两角和与差的余弦函数
专题:计算题,三角函数的求值
分析:依题意,可求得cosβ=-
,由于α=(α+β)-β,巧用两角差的余弦即可求得tan(α+β)的值.
| 4 |
| 5 |
解答:
解:∵sinβ=
,
<β<π,
∴cosβ=-
=-
,
又sin(α+β)=cosα
=cos[(α+β)-β]
=cos(α+β)cosβ+sin(α+β)sinβ
=-
cos(α+β)+
sin(α+β),
∴
sin(α+β)=-
cos(α+β),
∴tan(α+β)=-2.
故答案为:-2.
| 3 |
| 5 |
| π |
| 2 |
∴cosβ=-
| 1-sin2β |
| 4 |
| 5 |
又sin(α+β)=cosα
=cos[(α+β)-β]
=cos(α+β)cosβ+sin(α+β)sinβ
=-
| 4 |
| 5 |
| 3 |
| 5 |
∴
| 2 |
| 5 |
| 4 |
| 5 |
∴tan(α+β)=-2.
故答案为:-2.
点评:本题考查两角和与差的余弦函数,“凑角”是关键,考查三角函数间的关系式的应用,属于中档题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
如图是一几何体的三视图,则该几何体的表面积是( )


A、5+
| ||
B、5+2
| ||
C、4+2
| ||
D、4+2
|
椭圆
(φ为参数)的长轴长为( )
|
| A、3 | B、5 | C、6 | D、10 |
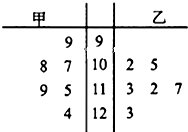 在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示: