题目内容
已知x∈[-
,
],
(1)求函数y=cosx的值域;
(2)求函数y=-3sin2x-4cosx+4的值域.
| π |
| 3 |
| 2π |
| 3 |
(1)求函数y=cosx的值域;
(2)求函数y=-3sin2x-4cosx+4的值域.
考点:三角函数的最值
专题:三角函数的求值
分析:(1)在单位圆中画出余弦函数线,直接由三角函数线得到函数y=cosx的值域;
(2)利用(1)中求出的cosx的范围,化正弦为余弦,配方后求函数y=-3sin2x-4cosx+4的值域.
(2)利用(1)中求出的cosx的范围,化正弦为余弦,配方后求函数y=-3sin2x-4cosx+4的值域.
解答:
解:(1)∵x∈[-
,
],
如图,
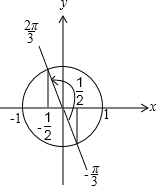
由余弦函数线可知,函数y=cosx的值域为[-
,1];
(2)y=-3sin2x-4cosx+4
=-3(1-cos2x)-4cosx+4
=3cos2x-4cosx+1
=3(cosx-
)2-
.
∵cosx∈[-
,1],
∴(cosx-
)2∈[0,
],
则3(cosx-
)2-
∈[-
,
].
∴函数y=-3sin2x-4cosx+4的值域是[-
,
].
| π |
| 3 |
| 2π |
| 3 |
如图,

由余弦函数线可知,函数y=cosx的值域为[-
| 1 |
| 2 |
(2)y=-3sin2x-4cosx+4
=-3(1-cos2x)-4cosx+4
=3cos2x-4cosx+1
=3(cosx-
| 2 |
| 3 |
| 1 |
| 3 |
∵cosx∈[-
| 1 |
| 2 |
∴(cosx-
| 2 |
| 3 |
| 49 |
| 36 |
则3(cosx-
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 15 |
| 4 |
∴函数y=-3sin2x-4cosx+4的值域是[-
| 1 |
| 3 |
| 15 |
| 4 |
点评:本题考查了利用三角函数线求余弦函数的值域,考查了配方法求函数的最值,考查了计算能力,是中档题.

练习册系列答案
相关题目
已知函数f(n)=log(n+1)(n+2)(n为正整数),若存在正整数k满足:f(1)•f(2)••f(n)=k,那么我们称k为“好整数”.当n∈[1,2013]时,则所有符合条件的“好整数”之和为( )
| A、54 | B、55 | C、65 | D、66 |
全集U=R,集合A={x|x>1},A={x|x<1},集合B={ x|y=
},则A∩B=( )
| 3-x |
| A、(-∞,0) |
| B、(-∞,1) |
| C、[1,+∞) |
| D、(1,3] |
设函数f(x)=log2|x|,则下列结论中正确的是( )
A、f(-1)<f(2)<f(-
| ||
B、f(-
| ||
C、f(2)<f(-
| ||
D、f(-1)<f(-
|