题目内容

已知{an}为等差数列，若a3+a4+a8=9，则前9项和S9=
 
．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：运用等差数列的通项公式，求得a1+4d=3，再由求和公式，化简代入数据即可得到．
解答： 解：设等差数列的公差为d，则a3+a4+a8=9，
即为a1+2d+a1+3d+a1+7d=9，
即3a1+12d=9，
即a1+4d=3，
则S9=9a1+
9×8
2
d=9（a1+4d）=9×3=27．
故答案为：27．
点评：本题考查等差数列的通项公式和求和公式的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
若非零向量
a
，
b
满足|
a
+
b
|=|
a
-
b
|=2|
b
|，则
a
+
b
与
a
-
b
的夹角是
 
．
下列几个命题：①不等式
3
x-1
＜x+1的解集为{x|x＜-2，或x＞2}；②已知a，b均为正数，且
1
a
+
4
b
=1，则a+b的最小值为9；③已知x，y均为正数，且x+3y-2=0，则3x+27y+1的最小值为7；其中正确的有
 
．（以序号作答）
已知m，n，l为两条不同的直线，α，β为两个不同的平面，给出下列4个命题：
①由α∥β，m?α，n?β，得m与n平行；
②由m∥n，m⊥α，n⊥l，得l∥α；
③由m⊥n，m∥α，得n⊥α；
④由m⊥α，n⊥β，α⊥β，l⊥m，得l∥n．
则正确命题的个数是（　　）
A、0B、1C、2D、3
若sin2θ=1，则tanθ+
cosθ
sinθ
的值是（　　）
A、2
B、-2
C、±2
D、
1
2
设等差数列{an}的前n项和为Sn，若a1=-11，a5=-3，则当Sn取最小值时，n等于
 
．
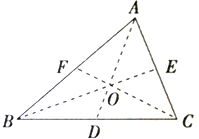如图，在△ABC中，D、E、F分别是BC、CA、AB的中点，O是三角形内一点．求证：
（1）若O是△ABC的重心，则
OA
+
OB
+
OC
=0；
（2）
AD
+
BE
+
CF
=0．
已知a、b、c、d为非负实数，f（x）=
ax+b
cx+d
（x∈R），且f（19）=19，f（97）=97，若x≠-
d
c
，对任意的实数x均有f（f（x））=x成立，试求出f（x）值域外的唯一数．
求下列函数的定义域：
（1）f（x）=lg（5x-2）
（2）f（x）=
3x+2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网