题目内容
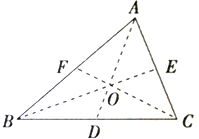如图，在△ABC中，D、E、F分别是BC、CA、AB的中点，O是三角形内一点．求证：（1）若O是△ABC的重心，则
| OA |
| OB |
| OC |
（2）
| AD |
| BE |
| CF |
考点：向量的加法及其几何意义
专题：平面向量及应用
分析：（1）利用三角形的重心性质、向量的平行四边形法则、向量共线定理即可得出；
（2）利用向量的平行四边形法则即可得出．
（2）利用向量的平行四边形法则即可得出．
解答：
证明：（1）∵O是△ABC的重心，∴
=2
，
+
=2
，
则
+
+
=-2
+2
=
．
（2）∵D、E、F分别是BC、CA、AB的中点，
∴
=
(
+
)，
=
(
+
)，
=
(
+
)，
∴
+
+
=
(
+
)+
(
+
)+
(
+
)=
．
| AO |
| OD |
| OB |
| OC |
| OD |
则
| OA |
| OB |
| OC |
| OD |
| OD |
| 0 |
（2）∵D、E、F分别是BC、CA、AB的中点，
∴
| AD |
| 1 |
| 2 |
| AB |
| AC |
| BE |
| 1 |
| 2 |
| BA |
| BC |
| CF |
| 1 |
| 2 |
| CA |
| CB |
∴
| AD |
| BE |
| CF |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| BA |
| BC |
| 1 |
| 2 |
| CA |
| CB |
| 0 |
点评：本题考查了三角形的重心性质、向量的平行四边形法则、向量共线定理，属于基础题．
练习册系列答案
相关题目
已知等差数列{an}的公差为2，若a1，a3，a4成等比数列，则a2的值为（ ）
| A、-4 | B、-10 | C、-8 | D、-6 |
已知集合A={y|y=-x2+3，x∈R}，B={x|y=
}，则A∩B=（ ）
| x+3 |
| A、{（0，3），（1，2）} |
| B、（-3，-3） |
| C、[-3，3] |
| D、{y|y≤3} |