题目内容
已知a、b、c、d为非负实数,f(x)=
(x∈R),且f(19)=19,f(97)=97,若x≠-
,对任意的实数x均有f(f(x))=x成立,试求出f(x)值域外的唯一数.
| ax+b |
| cx+d |
| d |
| c |
考点:函数的值
专题:计算题
分析:由题意先化简f(f(x))=x得:(a+d)cx2+(d2-a2)x-b(a+d)=0,由恒成立可得a+d=0,且d2-a2=0,即d=-a,再把f(19)=19,f(97)=97代入化简求出a、b、c、d的关系,从而求出f(x)的解析式,利用分裂常数法化简解析式后,即可得到答案.
解答:
解:由题设,对任意实数x≠-
有f(f(x))=x,即
=x,
化简,得(a+d)cx2+(d2-a2)x-b(a+d)=0,
由于上述方程对x≠-
恒成立,故a+d=0,且d2-a2=0,所以d=-a.…(10分)
又f(19)=19,f(97)=97,即19、97是方程
=x的两个根,
即方程是cx2+(d-a)x-b=0的两个根,
故由韦达定理,得
=116,-
=-1843,
结合d=-a,得a=58c,b=-1843c,d=-58c,
所以f(x)=
=58+
.
于是f(x)取不到58这个数,即58是f(x)值域外的唯一的数.…(20分)
| d |
| c |
a•
| ||
c•
|
化简,得(a+d)cx2+(d2-a2)x-b(a+d)=0,
由于上述方程对x≠-
| d |
| c |
又f(19)=19,f(97)=97,即19、97是方程
| ax+b |
| cx+d |
即方程是cx2+(d-a)x-b=0的两个根,
故由韦达定理,得
| a-d |
| c |
| d |
| c |
结合d=-a,得a=58c,b=-1843c,d=-58c,
所以f(x)=
| 58x-1843 |
| x-58 |
| 1521 |
| x-58 |
于是f(x)取不到58这个数,即58是f(x)值域外的唯一的数.…(20分)
点评:本题考查待定系数法求函数的解析式,函数恒成立问题,以及分裂常数法化简解析式,考查化简计算能力和逻辑思维能力,属于难题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2的值为( )
| A、-4 | B、-10 | C、-8 | D、-6 |
已知集合A={y|y=-x2+3,x∈R},B={x|y=
},则A∩B=( )
| x+3 |
| A、{(0,3),(1,2)} |
| B、(-3,-3) |
| C、[-3,3] |
| D、{y|y≤3} |
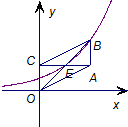 如图,面积为8的平行四边形OABC,对角线AC⊥OC,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1)的图象经过点E,B,则a=( )
如图,面积为8的平行四边形OABC,对角线AC⊥OC,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1)的图象经过点E,B,则a=( )