题目内容
求下列函数的定义域：
（1）f（x）=lg（5x-2）
（2）f（x）=
．
（1）f（x）=lg（5x-2）
（2）f（x）=
| 3x+2 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：（1）由对数式的真数大于0求解x的取值集合得答案；
（2）由根式内部的代数式大于等于0求解x的取值集合得答案．
（2）由根式内部的代数式大于等于0求解x的取值集合得答案．
解答：
解：（1）由5x-2＞0，得x＞
．
∴f（x）=lg（5x-2）的定义域为（
，+∞）；
（2）由3x+2≥0，得x≥-
．
∴f（x）=
的定义域为[-
，+∞）．
| 2 |
| 5 |
∴f（x）=lg（5x-2）的定义域为（
| 2 |
| 5 |
（2）由3x+2≥0，得x≥-
| 2 |
| 3 |
∴f（x）=
| 3x+2 |
| 2 |
| 3 |
点评：本题考查了函数的定义域及其求法，是基础的计算题．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知集合A={y|y=-x2+3，x∈R}，B={x|y=
}，则A∩B=（ ）
| x+3 |
| A、{（0，3），（1，2）} |
| B、（-3，-3） |
| C、[-3，3] |
| D、{y|y≤3} |
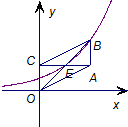如图，面积为8的平行四边形OABC，对角线AC⊥OC，AC与BO交于点E，某指数函数y=ax（a＞0，且a≠1）的图象经过点E，B，则a=（ ）