题目内容
若sin2θ=1，则tanθ+
的值是（ ）
| cosθ |
| sinθ |
| A、2 | ||
| B、-2 | ||
| C、±2 | ||
D、
|
考点：三角函数的化简求值
专题：三角函数的求值
分析：依题意，将所求关系式中的“切”化“弦”，通分后，利用同角三角函数间的关系式即可求得答案．
解答：
解：∵sin2θ=1，
∴tanθ+
=
+
=
=
=2，
故选：A．
∴tanθ+
| cosθ |
| sinθ |
| sinθ |
| cosθ |
| cosθ |
| sinθ |
| sin2θ+cos2θ |
| sinθcosθ |
| 1 | ||
|
故选：A．
点评：本题考查三角函数的化简求值，考查同角三角函数间的关系式的应用，属于基础题．
练习册系列答案
相关题目
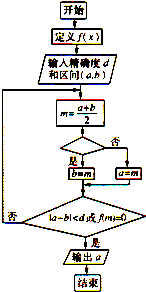已知图象不间断函数f（x）是区间[a，b]上的单调函数，且在区间（a，b）上存在零点．上图是用二分法求方程f（x）=0近似解的程序框图，判断框内可以填写的内容有如下四个选择：①f（a）f（m）＜0，
②f（a）f（m）＞0，
③f（b）f（m）＜0，
④f（b）f（m）＞0，
其中能够正确求出近似解的是（ ）
| A、①④ | B、②③ | C、①③ | D、②④ |
已知直线AB外的任一点O，下列条件中能确定点C与点A、B一定共线的是（ ）
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|