题目内容
下列几个命题:①不等式
<x+1的解集为{x|x<-2,或x>2};②已知a,b均为正数,且
+
=1,则a+b的最小值为9;③已知x,y均为正数,且x+3y-2=0,则3x+27y+1的最小值为7;其中正确的有 .(以序号作答)
| 3 |
| x-1 |
| 1 |
| a |
| 4 |
| b |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①不等式
<x+1化为(x+2)(x-1)(x-2)>0,利用“穿根法”解得x>2或-2<x<1,即可判断出;
②由于a,b均为正数,且
+
=1,变形为a+b=(a+b)(
+
)=5+
+
,再利用基本不等式的性质即可得出;
③由于x,y均为正数,且x+3y-2=0,利用基本不等式的性质可得3x+27y+1≥2
+1,即可得出.
| 3 |
| x-1 |
②由于a,b均为正数,且
| 1 |
| a |
| 4 |
| b |
| 1 |
| a |
| 4 |
| b |
| b |
| a |
| 4a |
| b |
③由于x,y均为正数,且x+3y-2=0,利用基本不等式的性质可得3x+27y+1≥2
| 3x•33y |
解答:
解:①不等式
<x+1化为(x+2)(x-1)(x-2)>0,解得x>2或-2<x<1,因此解集为{x|-2<x<1,或x>2},故不正确;
②∵a,b均为正数,且
+
=1,∴a+b=(a+b)(
+
)=5+
+
≥5+2
=9,当且仅当b=2a=6时取等号,因此最小值为9,正确;
③∵x,y均为正数,且x+3y-2=0,∴3x+27y+1≥2
+1=2
+1=7,当且仅当x=3y=1时取等号,因此其最小值为7,正确.
综上可得:其中正确的有 ②③.
故答案为:②③.
| 3 |
| x-1 |
②∵a,b均为正数,且
| 1 |
| a |
| 4 |
| b |
| 1 |
| a |
| 4 |
| b |
| b |
| a |
| 4a |
| b |
|
③∵x,y均为正数,且x+3y-2=0,∴3x+27y+1≥2
| 3x•33y |
| 32 |
综上可得:其中正确的有 ②③.
故答案为:②③.
点评:本题考查了“穿根法”解不等式、基本不等式的性质、简易逻辑的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
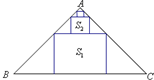 在等腰直角△ABC中,∠A=90°,BC=3,△ABC中排列着内接正方形,如图所示,若正方形的面积依次为S1,S2,…,Sn,…(从大到小),其中n∈N*,则
在等腰直角△ABC中,∠A=90°,BC=3,△ABC中排列着内接正方形,如图所示,若正方形的面积依次为S1,S2,…,Sn,…(从大到小),其中n∈N*,则| lim |
| n→∞ |
已知集合A={y|y=-x2+3,x∈R},B={x|y=
},则A∩B=( )
| x+3 |
| A、{(0,3),(1,2)} |
| B、(-3,-3) |
| C、[-3,3] |
| D、{y|y≤3} |