题目内容
已知函数f（3x）=log2
，则f（
）的值是（ ）
|
| 7 |
| 3 |
A、
| ||
| B、1 | ||
C、log2
| ||
| D、2 |
考点：对数的运算性质
专题：函数的性质及应用
分析：利用函数性质和对数性质求解．
解答：
解：∵f（3x）=log2
，
∴f（
）=f（3×
）=log2
=log22=1．
故选：B．
|
∴f（
| 7 |
| 3 |
| 7 |
| 9 |
|
故选：B．
点评：本题考查函数值的求法，解题时要认真审题，注意对数性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
若m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中的真命题是（ ）
| A、若m?β，α⊥β，则m⊥α |
| B、若α∩γ=m，β∩γ=n，m∥n，则α∥β |
| C、若m⊥β，m∥α，则α⊥β |
| D、若α⊥γ，α⊥β，则β⊥γ |
已知向量
=（-1，2），
=（5，k），若
∥
，则实数k的值为（ ）
| a |
| b |
| a |
| b |
| A、5 | B、-5 | C、10 | D、-10 |
若不等式x2+ax+1≥0对一切x∈（0，
]成立，则a的最小值为（ ）
| 1 |
| 2 |
A、-
| ||
| B、0 | ||
| C、-2 | ||
| D、-3 |
函数y=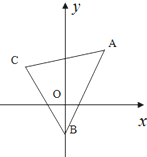
如图，已知三角形的顶点为A（2，4），B（0，-2），C（-2，3）．求：