题目内容
已知函数f(x)=sinx•cosx,x∈R,给出下列四个命题:①f(x)是奇函数;②f(x)的图象关于直线x=
对称;③f(x)在区间(-
,
)上是增函数;④f(x)的值域是[-
,
].其中正确命题的序号是 (注:把你认为正确命题的序号填在横线上)
| 3 |
| 5 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
考点:二倍角的正弦
专题:三角函数的图像与性质
分析:函数f(x)=sinx•cosx=
sin2x,x∈R,下列四个命题:
①由f(-x)=-f(x),即可得出奇偶性;
②sin2x=±1,解得x=
(k∈Z),可得f(x)的图象的对称轴;
③若x∈(-
,
),则2x∈(-
,
),因此f(x)在区间(-
,
)上是增函数;
④由于sin2x∈[-1,1],可得f(x)的值域是[-
,
].
| 1 |
| 2 |
①由f(-x)=-f(x),即可得出奇偶性;
②sin2x=±1,解得x=
| kπ |
| 4 |
③若x∈(-
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
④由于sin2x∈[-1,1],可得f(x)的值域是[-
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:函数f(x)=sinx•cosx=
sin2x,x∈R,下列四个命题:
①∵f(-x)=-f(x),∴f(x)是奇函数,正确;
②sin2x=±1,解得x=
(k∈Z),可得f(x)的图象关于直线x=
(k∈Z)对称,因此不正确;
③若x∈(-
,
),则2x∈(-
,
),因此f(x)在区间(-
,
)上是增函数,正确;
④∵sin2x∈[-1,1],∴f(x)的值域是[-
,
],正确.
其中正确命题的序号是①③④.
故答案为:①③④.
| 1 |
| 2 |
①∵f(-x)=-f(x),∴f(x)是奇函数,正确;
②sin2x=±1,解得x=
| kπ |
| 4 |
| kπ |
| 4 |
③若x∈(-
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
④∵sin2x∈[-1,1],∴f(x)的值域是[-
| 1 |
| 2 |
| 1 |
| 2 |
其中正确命题的序号是①③④.
故答案为:①③④.
点评:本题考查了三角函数的图象与性质、倍角公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)( )
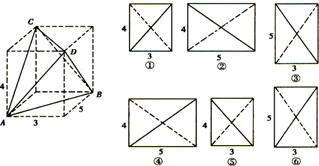

| A、①②⑥ | B、①②③ |
| C、④⑤⑥ | D、③④⑤ |