题目内容
设函数f(x)=cos(?x+
)•sin(?x-
)+cos2?x-
(?>0)图象上的相邻的最高点与最低点之间的距离为
.
(1)求?的值及单调递增区间;
(2)设△ABC的内角A、B、C的对边分别为a,b,c,且b+c=2,A=
,求f(a)的值域.
| π |
| 3 |
| π |
| 2 |
| 1 |
| 4 |
| 2 |
(1)求?的值及单调递增区间;
(2)设△ABC的内角A、B、C的对边分别为a,b,c,且b+c=2,A=
| π |
| 3 |
考点:余弦定理的应用,三角函数中的恒等变换应用
专题:三角函数的图像与性质,解三角形
分析:(1)先化简求得解析式f(x)=
sin(2ωx+
),由周期公式可求得ω的值,由正弦函数的图象和性质可求得单调递增区间;
(2)由余弦定理可求得a2=4-3bc,由2=b+c≥2
可求得1≤a≤2,由f(a)=
sin(πa+
),从而求得f(a)的值域.
| 1 |
| 2 |
| π |
| 6 |
(2)由余弦定理可求得a2=4-3bc,由2=b+c≥2
| bc |
| 1 |
| 2 |
| π |
| 6 |
解答:
解:(1)f(x)=
sin(2ωx+
),…(2分)
由条件,T=2=
⇒ω=
.
∴f(x)=
sin(πx+
)…(4分)
令2kπ-
≤(πx+
)≤2kπ+
,k∈Z…(5分)
解得单调递增区间:[2k-
,2k+
]k∈Z…(6分)
(2)由余弦定理:∵A=
∴a2=b2+c2-2bccosA=(b+c)2-3bc=4-3bc…(7分)
又2=b+c≥2
⇒0<bc≤1,故1≤a2<4,
又2=b+c>a,故1≤a≤2 …(9分)
由f(a)=
sin(πa+
),
≤πa+
<
,所以f(a)的值域为[-
,
].…(12分)
| 1 |
| 2 |
| π |
| 6 |
由条件,T=2=
| 2π |
| 2ω |
| π |
| 2 |
∴f(x)=
| 1 |
| 2 |
| π |
| 6 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得单调递增区间:[2k-
| 2 |
| 3 |
| 1 |
| 3 |
(2)由余弦定理:∵A=
| π |
| 3 |
∴a2=b2+c2-2bccosA=(b+c)2-3bc=4-3bc…(7分)
又2=b+c≥2
| bc |
又2=b+c>a,故1≤a≤2 …(9分)
由f(a)=
| 1 |
| 2 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| 13π |
| 6 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题主要考查了余弦定理的应用,三角函数中的恒等变换应用,三角函数的图象与性质,考查了转化思想,属于中档题.

练习册系列答案
相关题目
如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)( )
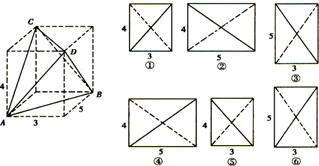

| A、①②⑥ | B、①②③ |
| C、④⑤⑥ | D、③④⑤ |