题目内容
已知函数f(x)=
(Ⅰ)求f(-
)的值;
(Ⅱ)当x∈[0,
)时,求g(x)=f(x)+sin2x的最大值和最小值.
| 4cos4x-2cos2x-1 |
| cos2x |
(Ⅰ)求f(-
| 11π |
| 12 |
(Ⅱ)当x∈[0,
| π |
| 4 |
考点:三角函数的最值,三角函数中的恒等变换应用
专题:三角函数的求值
分析:(I)由三角函数公式化简可得f(x)=cos2x,代值计算可得;
(Ⅱ)由(Ⅰ)可得g(x)=
sin(2x+
),由x∈[0,
)和三角函数的值域可得.
(Ⅱ)由(Ⅰ)可得g(x)=
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:
解:(I)化简可得f(x)=
=
=
=2cos2x+1-2=2cos2x-1=cos2x,
∴f(-
)=cos(-
)=cos
=
;
(Ⅱ)由(Ⅰ)可得g(x)=f(x)+sin2x
=cos2x+sin2x=
sin(2x+
),
∵x∈[0,
),∴2x+
∈[
,
),
∴sin(2x+
)∈[
,1],
∴
sin(2x+
)∈[1,
],
∴g(x)的最小值是1,最大值是
| 4cos4x-2cos2x-1 |
| cos2x |
=
| (2cos2x-1)(2cos2x+1)-2cos2x |
| cos2x |
=
| cos2x(2cos2x+1)-2cos2x |
| cos2x |
=2cos2x+1-2=2cos2x-1=cos2x,
∴f(-
| 11π |
| 12 |
| 11π |
| 6 |
| π |
| 6 |
| ||
| 2 |
(Ⅱ)由(Ⅰ)可得g(x)=f(x)+sin2x
=cos2x+sin2x=
| 2 |
| π |
| 4 |
∵x∈[0,
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴sin(2x+
| π |
| 4 |
| ||
| 2 |
∴
| 2 |
| π |
| 4 |
| 2 |
∴g(x)的最小值是1,最大值是
| 2 |
点评:本题考查三角函数的最值,熟练应用公式化简已知函数是解决问题的关键,属中档题.

练习册系列答案
相关题目
已知tanα,tanβ是关于x的方程x2+(logaM+logbM)x-logaM•logbM=0的两个根,其中a、b,M均为不等于1的正数,若sinαcosβ+cosαsinβ=2sinαsinβ,则a,b,M满足的关系是( )
A、
| ||
B、
| ||
| C、a+b=M | ||
| D、ab=M |
函数f(x)=sinx的图象与g(x)=cosx的图象关于某条直线对称,这条直线可以是( )
A、x=
| ||
B、x=
| ||
C、x=-
| ||
D、x=-
|
如图是某几何体的三视图,则该几何体的体积为( )
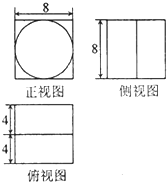

| A、256+128π |
| B、256+64π |
| C、64+64π |
| D、64+32π |
已知复数z=
,i是虚数单位,则复数虚部是( )
| 1+2i |
| 3-i |
A、
| ||
B、
| ||
C、
| ||
D、
|
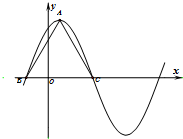 函数f(x)=6cos2
函数f(x)=6cos2