题目内容
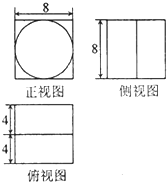
如图是某几何体的三视图，则该几何体的体积为（ ）
| A、256+128π |
| B、256+64π |
| C、64+64π |
| D、64+32π |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知的三视图可得：该几何体是一个圆柱和长方体的组合体，分别求出圆柱和长方体的体积，相加可得答案．
解答：
解：由已知的三视图可得：该几何体是一个圆柱和长方体的组合体，
圆柱的底面直径为8，半径为4，高为8，故体积为：64π，
长方体的长，宽，高分别为：8，8，4，体积为：256，
故几何体的体积V=256+64π，
故选：B
圆柱的底面直径为8，半径为4，高为8，故体积为：64π，
长方体的长，宽，高分别为：8，8，4，体积为：256，
故几何体的体积V=256+64π，
故选：B
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
若一个几何体的三视图如图所示，则其体积为（ ）
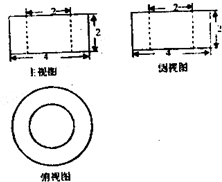
| A、5π | B、6π | C、7π | D、8π |
函数f（x）=Acos（ωx+φ）（A＞0，ω＞0）在x=3处取最大值，则（ ）
| A、f（x-3）一定是奇函数 |
| B、f（x-3）一定是偶函数 |
| C、f（x+3）一定是奇函数 |
| D、f（x+3）一定是偶函数 |
设a∈R，则“a=1”是直线“l1：ax+2y-1=0与直线l2：（a+1）x-y+4=0垂直”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
已知变量x，y之间具有相关关系，其散点图如图所示，则其回归直线方程可能是（ ）
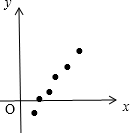
| A、y=2x-1 |
| B、y=2x+1 |
| C、y=-2x+1 |
| D、y=-2x-1 |