题目内容
设函数f(x)=x2+ax+b的值域为A,关于x的不等式f(x)<c的解集为B.
(1)若a=4,b=-2.c=3,求集合A与B;
(2)若A=[0,+∞),B=(m,m+6),求实数c的值.
(1)若a=4,b=-2.c=3,求集合A与B;
(2)若A=[0,+∞),B=(m,m+6),求实数c的值.
考点:一元二次不等式的解法,二次函数的性质
专题:函数的性质及应用,不等式的解法及应用
分析:(1)a=4,b=-2,c=3时,求出f(x)的值域A与不等式f(x)<c的解集B;
(2)根据f(x)的值域A得出△=0①,不等式f(x)<c的解集为B得出a2-4(b-c)=62②;由①②求出c的值.
(2)根据f(x)的值域A得出△=0①,不等式f(x)<c的解集为B得出a2-4(b-c)=62②;由①②求出c的值.
解答:
解:(1)a=4,b=-2,c=3时,
f(x)=x2+4x-2=(x+2)2-6≥-6;
∴函数的值域为A=[-6,+∞);
又∵f(x)<c,
∴x2+4x-5<0,
解得-5<x<1;
∴不等式的解集为B=(-5,1);
(2)∵A=[0,+∞),
∴f(x)=x2+ax+b≥0,
即△=a2-4b=0①;
又设f(x)-c=x2+ax+b-c=0的两个实数根为x1、x2,
且B=(m,m+6),
∴(x1-x2)2=a2-4(b-c)②;
由①②知,62=4c,
∴c=9.
f(x)=x2+4x-2=(x+2)2-6≥-6;
∴函数的值域为A=[-6,+∞);
又∵f(x)<c,
∴x2+4x-5<0,
解得-5<x<1;
∴不等式的解集为B=(-5,1);
(2)∵A=[0,+∞),
∴f(x)=x2+ax+b≥0,
即△=a2-4b=0①;
又设f(x)-c=x2+ax+b-c=0的两个实数根为x1、x2,
且B=(m,m+6),
∴(x1-x2)2=a2-4(b-c)②;
由①②知,62=4c,
∴c=9.
点评:本题考查了函数的性质与应用问题,也考查了不等式的解法与应用问题,是综合性题目.

练习册系列答案
相关题目
已知f(x)=(sinx+cosx)sinx,若f(x1)≤f(x)≤f(x2),对?x∈R成立,则|x1-x2|最小值为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |
已知梯形ABCD中,AB∥CD,∠B=
,DC=2AB=2BC=2,以对角线AC为旋转轴旋转一周得到的几何体的表面积为( )
| π |
| 2 |
A、2(1+
| ||||
B、2
| ||||
C、
| ||||
D、(3+2
|
若一个几何体的三视图如图所示,则其体积为( )
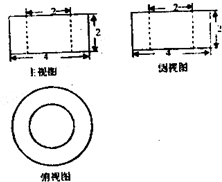

| A、5π | B、6π | C、7π | D、8π |
若函数f(x)=sinxcosx,下列结论中正确的是( )
| A、函数f(x)的图象关于原点对称 |
| B、函数f(x)最小正周期为2π |
| C、函数f(x)为偶函数 |
| D、函数f(x)的最大值为1 |