题目内容
已知二次函数y=f(x)的图象为开口向下的抛物线,且对任意x∈R都有f(1+x)=f(1-x).若向量
=(m,-1),
=(m,-2),则满足不等式f(
•
)>f(-1)的m的取值范围为 .
| a |
| b |
| a |
| b |
考点:平面向量的综合题,二次函数的性质
专题:综合题,平面向量及应用
分析:由已知中二次函数y=f(x)的图象为开口向下的抛物线,且对任意x∈R都有f(1-x)=f(1+x).我们可以判断函数的图象是以x=1为对称轴,开口方向朝下的抛物线,再由向量
=(m,-1),
=(m,-2),结合 二次函数的性质和向量数量积运算,我们可以得到一个关于m的不等式,解不等式即可求出m的取值范围.
| a |
| b |
解答:
解:∵对任意x∈R都有f(1-x)=f(1+x).
故函数的对称轴为x=1,
∵
=(m,-1),
=(m,-2),
∴
=m2+2,
∴|m2+2-1|<|-1-1|
解得-1<m<1
故答案为:(-1,1)
故函数的对称轴为x=1,
∵
| a |
| b |
∴
| a• |
| b |
∴|m2+2-1|<|-1-1|
解得-1<m<1
故答案为:(-1,1)
点评:本题考查的知识点是二次函数的性质,绝对值不等式的解法,平面向量的数量积的运算,其中根据二次函数的性质和向量数量积运算,将不等式f(
•
)>f(-1)转化为一个关于m的不等式,是解答本题的关键.
| a |
| b |

练习册系列答案
相关题目
已知数列{an}的通项公式是an=n2sin(
π),则a1+a2+a3+…+a2014=( )
| 2n+1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 在过正方体AC1的8个顶点中的3个顶点的平面中,能与三条棱CD、A1D1、BB1所成的角均相等的平面共有( )
在过正方体AC1的8个顶点中的3个顶点的平面中,能与三条棱CD、A1D1、BB1所成的角均相等的平面共有( )| A、1个 | B、4个 | C、8个 | D、12个 |
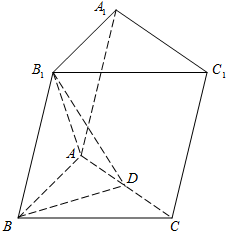 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D. 如图正方体ABCD-A1B1C1D1,下面结论正确的是
如图正方体ABCD-A1B1C1D1,下面结论正确的是