题目内容
设向量
=(m,1),
=(2,-3),若
∥
,则实数m的值为( )
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:平面向量的坐标运算,平行向量与共线向量
专题:平面向量及应用
分析:由向量平行可得m的方程,解方程可得.
解答:
解:∵
=(m,1),
=(2,-3),且
∥
,
∴-3m-2×1=0,解得m=-
故选:D
| a |
| b |
| a |
| b |
∴-3m-2×1=0,解得m=-
| 2 |
| 3 |
故选:D
点评:本题考查向量的平行关系,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在等比数列{an}中,a1=2,q=3,则a3=( )
| A、6 | B、8 | C、12 | D、18 |
方程x2-px+6=0的解集为M,方程x2+6x-q=0的解集为N,且M∩N={2},那么p+q=( )
| A、21 | B、8 | C、6 | D、7 |
b>0是函数f(x)=x2+bx+c在[0,+∞)单调的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知等差数列{an}的前n项和Sn,满足Sn=-
n2+2n,则Sn的最大值为( )
| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
若奇函数f(x)在区间[3,7]上是减函数且有最大值4,则f(x)在区间[-7,-3]上是( )
| A、增函数且最小值为-4 |
| B、增函数且最大值为-4 |
| C、减函数且最小值为-4 |
| D、减函数且最大值为-4 |
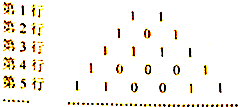 将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是
将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是