题目内容
已知AD是△ABC的角平分线，且AC=2，AB=3，A=60°，则AD长为 ．
考点：余弦定理
专题：解三角形
分析：由条件利用余弦定理求得BC、cosB的值，再根据角平分线的性质求得BD的值，再利用余弦定理求得AD的值．
解答：
解：△ABC中，由余弦定理可得BC2=AB2+AC2-2AB•AC•cosA=4+9-12cos60°=7，∴BC=
，
∴cosB=
=
=
．
再根据角平分线的性质可得
=
=
，∴BD=
BC=
．
∴AD2=AB2+BD2-2AB•BD•cosB=9+
-
×
=
，∴AD=
，
故答案为：
．
| 7 |
∴cosB=
| AB2+BC2-AC2 |
| 2AB•BC |
| 9+7-4 | ||
6
|
2
| ||
| 7 |
再根据角平分线的性质可得
| CD |
| BD |
| AC |
| AB |
| 2 |
| 3 |
| 3 |
| 5 |
3
| ||
| 5 |
∴AD2=AB2+BD2-2AB•BD•cosB=9+
| 63 |
| 25 |
18
| ||
| 5 |
2
| ||
| 7 |
| 108 |
| 25 |
6
| ||
| 5 |
故答案为：
6
| ||
| 5 |
点评：本题主要考查余弦定理的应用，角平分线的性质，属于基础题．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
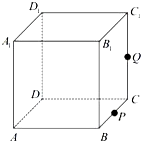如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则下列命题正确的是已知集合A={x|（x+1）（-x+2）≥0}，集合B为整数集，则A∩B=（ ）
| A、{-1，0} |
| B、{0，1} |
| C、{-2，-1，0，1} |
| D、{-1，0，1，2} |
设向量
=（m，1），
=（2，-3），若
∥
，则实数m的值为（ ）
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、-
|