题目内容
在等比数列{an}中,a1=2,q=3,则a3=( )
| A、6 | B、8 | C、12 | D、18 |
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:利用等比数列的性质求解.
解答:
解:∵在等比数列{an}中,a1=2,q=3,
a3=2×32=18.
故选:D.
a3=2×32=18.
故选:D.
点评:本题考查等比数列的第18项的求法,是基础题,解题时要注意等比数列的通项公式的合理运用.

练习册系列答案
相关题目
函数f(x)=-sinx+1的图象大致为( )
A、 |
B、 |
C、 |
D、 |
f(x)的定义域为R,f(2+x)=f(2-x),-1<x<2时,f(x)=(
)x,则有( )
| 1 |
| 2 |
A、f(-
| ||
B、f(4)<f(1)<f(-
| ||
C、f(1)<f(-
| ||
D、f(1)<f(4)<f(-
|
已知集合A={x|(x+1)(-x+2)≥0},集合B为整数集,则A∩B=( )
| A、{-1,0} |
| B、{0,1} |
| C、{-2,-1,0,1} |
| D、{-1,0,1,2} |
设向量
=(m,1),
=(2,-3),若
∥
,则实数m的值为( )
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
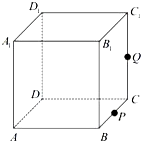 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是