题目内容
设数列{an}的首项a1=
,前n项和为Sn,且满足2an+1+Sn=3(n∈N*).
(Ⅰ)求a2及an;
(Ⅱ)求证:anSn≤
.
| 3 |
| 2 |
(Ⅰ)求a2及an;
(Ⅱ)求证:anSn≤
| 9 |
| 4 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由2an+1+Sn=3,得2a2+a1=3,由此能求出a2=
;由2an+1+Sn=3,2an+Sn-1=3(n≥2)相减,推导出数列{an}是以
为首项,以
为公比的等比数列,由此能求出an.
(Ⅱ)由(Ⅰ)得Sn=3[1-(
)n],由此能证明anSn≤
.
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)得Sn=3[1-(
| 1 |
| 2 |
| 9 |
| 4 |
解答:
(Ⅰ)解:由2an+1+Sn=3,得2a2+a1=3,
又a1=
,所以a2=
.(2分)
由2an+1+Sn=3,2an+Sn-1=3(n≥2)相减,
得
=
,又
=
,
所以数列{an}是以
为首项,以
为公比的等比数列.(5分)
因此an=
•(
)n-1=3•(
)n(n∈N*).(7分)
(Ⅱ)证明:由(Ⅰ),得Sn=3-2an+1=3-2•3(
)n+1=3[1-(
)n],(9分)
因为anSn=3•(
)n•3[1-(
)n]≤9•(
)2=
(12分)
当且仅当(
)n=1-(
)n时,
即n=1时,取等号.所以anSn≤
.(14分)
又a1=
| 3 |
| 2 |
| 3 |
| 4 |
由2an+1+Sn=3,2an+Sn-1=3(n≥2)相减,
得
| an+1 |
| an |
| 1 |
| 2 |
| a2 |
| a1 |
| 1 |
| 2 |
所以数列{an}是以
| 3 |
| 2 |
| 1 |
| 2 |
因此an=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)证明:由(Ⅰ),得Sn=3-2an+1=3-2•3(
| 1 |
| 2 |
| 1 |
| 2 |
因为anSn=3•(
| 1 |
| 2 |
| 1 |
| 2 |
(
| ||||
| 2 |
| 9 |
| 4 |
当且仅当(
| 1 |
| 2 |
| 1 |
| 2 |
即n=1时,取等号.所以anSn≤
| 9 |
| 4 |
点评:本题考查数列的第2项及通项公式的求法,考查不等式的证明,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知角α的终边经过P(-3,4),则cos2α+sin2α=( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
抛物线y=mx2的焦点与椭圆
+
=1的上焦点重合,则m=( )
| y2 |
| 6 |
| x2 |
| 2 |
A、
| ||
B、
| ||
| C、8 | ||
| D、4 |
已知f(x)为R上的偶函数,且f(1)=0,当x1,x2∈[0,+∞)且x1<x2时,有f(x1)<f(x2),则不等式
<0的解为( )
| f(x)+2•f(-x) |
| x |
| A、(-1,1) |
| B、(-∞,-1)∪(1,+∞) |
| C、(-∞,-1)∪(0,1) |
| D、(-1,0)∪(1,+∞) |
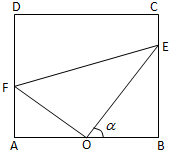 合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50
合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50