题目内容
对于实数x,将满足“0≤y<1且x-y为整数”的实数y称为实数x的小数部分,用符号<x>表示.已知无穷数列{an}满足如下条件:
①a1=<a>;②an+1=
.
(1)当a=
时,数列{an}通项公式为 ;
(2)当a>
时,对任意n∈N*都有an=a-1,则a的值为 .
①a1=<a>;②an+1=
|
(1)当a=
| 3 |
(2)当a>
| 3 |
| 2 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:(1)当a=
时,a1=<
>=
-1.由<x>的意义可得a2=
,a3=
-1.即可得出通项公式.
(2)由于对任意n∈N*都有an=a-1,a>
,可得
<a-1<1,1<
<2.因此a2=<
>=
-1=a-1,解出即可.
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
(2)由于对任意n∈N*都有an=a-1,a>
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| a-1 |
| 1 |
| a-1 |
| 1 |
| a-1 |
解答:
解:(1)当a=
时,a1=<
>=
-1.
∴a2=<
>=<
>=
,
∴a3=<
>=<
+1>=
-1.
∴数列{an}通项公式为an=
.
(2)∵对任意n∈N*都有an=a-1,a>
,
可得0≤a-1<1,a>
,
∴
<a-1<1,
∴1<
<2.
∴a2=<
>=
-1=a-1,
化为a2-a-1=0,
解得a=
.
故答案分别为:(1)an=
.
(2)
.
| 3 |
| 3 |
| 3 |
∴a2=<
| 1 | ||
|
| ||
| 2 |
| ||
| 2 |
∴a3=<
| 2 | ||
|
| 3 |
| 3 |
∴数列{an}通项公式为an=
|
(2)∵对任意n∈N*都有an=a-1,a>
| 3 |
| 2 |
可得0≤a-1<1,a>
| 3 |
| 2 |
∴
| 1 |
| 2 |
∴1<
| 1 |
| a-1 |
∴a2=<
| 1 |
| a-1 |
| 1 |
| a-1 |
化为a2-a-1=0,
解得a=
| ||
| 2 |
故答案分别为:(1)an=
|
(2)
| ||
| 2 |
点评:本题考查了新定义<x>的计算方法、递推式的意义,考查了推理能力,属于难题.

练习册系列答案
相关题目
三个数0.993.3,log3π,log20.8的大小关系为( )
| A、log3π<0.993.3<log20.8 |
| B、log20.8<log3π<0.993.3 |
| C、0.993.3<log20.8 l<og3π |
| D、log20.8<0.993.3<log3π |
已知P为椭圆
+
=1上的点,F1、F2为其两焦点,则使∠F1PF2=90°的点P有( )
| x2 |
| 16 |
| y2 |
| 12 |
| A、4个 | B、2个 | C、1个 | D、0个 |
如果曲线C上任意一点的坐标都是方程F(x,y)=0的解,那么下列命题正确的是( )
| A、曲线C的方程是F(x,y)=0 |
| B、曲线C上的点都在方程F(x,y)=0的曲线上 |
| C、方程F(x,y)=0的曲线是C |
| D、以方程F(x,y)=0解为坐标点都在曲线C上 |
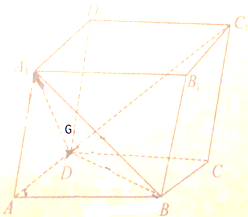 如图,在平行六面体ABCD-A1B1C1D1中,G为△A1BD的重心,设
如图,在平行六面体ABCD-A1B1C1D1中,G为△A1BD的重心,设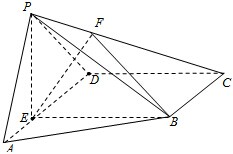 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.