题目内容

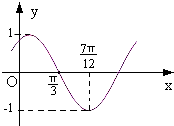已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜
π
2
）的图象如图所示，则ω和φ的值分别为（　　）
A、ω=1，φ=
π
6
B、ω=2，φ=
π
6
C、ω=1，φ=
π
3
D、ω=2，φ=
π
3
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：直接利用函数的图象先确定周期，进一步利用函数值确定 Φ的值．
解答： 解：根据函数的图象T=4×（
7π
12
-
π
3
）=π，所以ω=
2π
π
=2，
当x=
π
3
时函数值为0，
∴sin（
2π
3
+φ）=0
∴φ=kπ-
2π
3
，k∈Z
由于0＜φ＜
π
2
，
所以φ=
π
3
，
故选：D．
点评：本题主要考察了由y=Asin（ωx+φ）的部分图象确定其解析式，属于基础题．
练习册系列答案
相关题目
设函数f（x）=
a
x2
+lnx，g（x）=x3-x2-3．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）若存在x1，x2∈[-
1
3
，3]，使得g（x1）-g（x2）≥M成立，求满足条件的最大整数M；
（Ⅲ）如果对任意的s，t∈[
1
3
，2]，都有sf（s）≥g（t）成立，求实数a的取值范围．
计算：
(2a
2
3
b
1
2
)(-6a
1
2
b
1
3
)
-4a
1
6
b
5
6
．
若集合{4，2}与集合B={2，a2}相等，则实数a的值为
 
．
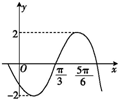已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-π＜φ＜0）的部分图象如图，则f（x）的表达式为（　　）
A、f（x）=2sin（
1
2
x-
2
3
π）
B、f（x）=2sin（x-
2
3
π）
C、f（x）=2sin（
1
2
x+
π
3
）
D、f（x）=2sin（2x-
2
3
π）
已知函数g（x）对一切实数x，y都有g（x+y）-g（y）-x（x+2y+1）成立，是g（x）=0，且f（x）=
g(x)-3x+3
x
．
（1）求g（0）的值；
（2）求f（x）的解析式；
（3）已知k∈R，设P：不等式f（2x）-k•2x≥0在x∈[-1，1]上有解，Q：f（|2x-1|）+k•
2
|2x-1|
-3k=0有三个不同的实数解，如果满足P成立的k的集合记为A，满足Q成立的k的集合记为B，求A∩B．
设点P（x，y）满足条件
x≤0
y≥0
y≤2x+2
，点Q（a，b）（a≤0，b≥0）满足
OP
•
OQ
≤1恒成立，其中O是坐标原点，则Q点的轨迹所围成图形的面积是
 
．
对任意的x∈[-2，1]时，不等式x2+2x-a≤0恒成立，则实数a的取值范围是（　　）
A、（-∞，0]
B、（-∞，3]
C、[0，+∞）
D、[3，+∞）
某几何体的三视图如图所示，其中俯视图是个半圆，则该几何体的表面积为（　　）
A、
5π
2
+
3
B、
5π
2
C、
3π
2
+
3
D、
3π
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网