题目内容
已知函数g(x)对一切实数x,y都有g(x+y)-g(y)-x(x+2y+1)成立,是g(x)=0,且f(x)=
.
(1)求g(0)的值;
(2)求f(x)的解析式;
(3)已知k∈R,设P:不等式f(2x)-k•2x≥0在x∈[-1,1]上有解,Q:f(|2x-1|)+k•
-3k=0有三个不同的实数解,如果满足P成立的k的集合记为A,满足Q成立的k的集合记为B,求A∩B.
| g(x)-3x+3 |
| x |
(1)求g(0)的值;
(2)求f(x)的解析式;
(3)已知k∈R,设P:不等式f(2x)-k•2x≥0在x∈[-1,1]上有解,Q:f(|2x-1|)+k•
| 2 |
| |2x-1| |
考点:抽象函数及其应用,函数最值的应用
专题:函数的性质及应用
分析:(1)对抽象函数满足的函数值关系的理解和把握是解决该问题的关键,对自变量适当的赋值可以解决该问题,结合已知条件可以赋x=-1,y=1求出f(0);
(2)在(1)基础上赋值y=0可以实现求解f(x)的解析式的问题;
(3)利用分离参数法,求出函数的最值,即可求出集合A,方程f(|2x-1|)+k•
-3k=0⇒|2x-1|2-(2+3k)|2x-1|+(1+2k)=0,(|2x-1|≠0),令|2x-1|=t,则t2-(2+3k)t+(1+2k)=0(t≠0),构造函数h(t)=t2-(2+3k)t+(1+2k),通过数形结合与等价转化的思想即可求得k的范围,继而的都集合B,再根据交集的运算求出结果
(2)在(1)基础上赋值y=0可以实现求解f(x)的解析式的问题;
(3)利用分离参数法,求出函数的最值,即可求出集合A,方程f(|2x-1|)+k•
| 2 |
| |2x-1| |
解答:
解:(1)∵g(x+y)-g(y)=x(x+2y+1),g(1)=0,
令x=1,y=0,得g(1)-g(0)=1×(1+0+1)=2,
故g(0)=-2,
(2)令y=0,则g(x)-g(0)=x(x+1),
∴g(x)=x2+x-2,
∴f(x)=
=x+
-2
(3)∵f(2x)-k•2x≥0
∴k≤
=(
)2-2(
)+1,
设
=t,t∈[
,2],
∴k≤(t-1)2,
∵(t-1)2max=1,
∴k≤1,
∴A=(-∞,1],
∵f(|2x-1|)+k•
-3k=0可化为:
|2x-1|2-(2+3k)|2x-1|+(1+2k)=0,|2x-1|≠0,
令|2x-1|=t,则方程化为t2-(2+3k)t+(1+2k)=0(t≠0),
∵f(|2x-1|)+k•
-3k=0有三个不同的实数解,
∴由t=|2x-1|的图象知,
t2-(2+3k)t+(1+2k)=0(t≠0),有两个根t1、t2,
且0<t1<1<t2或0<t1<1,t2=1.
记h(t)=t2-(2+3k)t+(1+2k),
由题意可知,
或
解得k>0,
∴B=(0,+∞)
∴A∩B=(0,1]
令x=1,y=0,得g(1)-g(0)=1×(1+0+1)=2,
故g(0)=-2,
(2)令y=0,则g(x)-g(0)=x(x+1),
∴g(x)=x2+x-2,
∴f(x)=
| g(x)-3x+3 |
| x |
| 1 |
| x |
(3)∵f(2x)-k•2x≥0
∴k≤
| f(2x) |
| 2x |
| 1 |
| 2x |
| 1 |
| 2x |
设
| 1 |
| 2x |
| 1 |
| 2 |
∴k≤(t-1)2,
∵(t-1)2max=1,
∴k≤1,
∴A=(-∞,1],
∵f(|2x-1|)+k•
| 2 |
| |2x-1| |
|2x-1|2-(2+3k)|2x-1|+(1+2k)=0,|2x-1|≠0,
令|2x-1|=t,则方程化为t2-(2+3k)t+(1+2k)=0(t≠0),
∵f(|2x-1|)+k•
| 2 |
| |2x-1| |
∴由t=|2x-1|的图象知,
t2-(2+3k)t+(1+2k)=0(t≠0),有两个根t1、t2,
且0<t1<1<t2或0<t1<1,t2=1.
记h(t)=t2-(2+3k)t+(1+2k),
由题意可知,
|
|
解得k>0,
∴B=(0,+∞)
∴A∩B=(0,1]
点评:本题考查函数的单调性,考查函数的最值,考查分离参数法求解恒成立问题,考查函数与方程思想,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数f(x)=x2-2(1-a2)x-a在区间(1,3)内有零点,则实数a的取值范围是( )
A、(0,
| ||
B、(-1,-
| ||
| C、(-1,1) | ||
D、(-
|
设函数f(x)=ax(a>0且a≠1),f(2)=9,则f(
)=( )
| 1 |
| 2 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
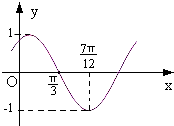 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<| π |
| 2 |
A、ω=1,φ=
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=
| ||
D、ω=2,φ=
|
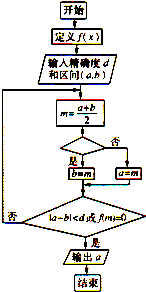 已知图象不间断函数f(x)是区间[a,b]上的单调函数,且在区间(a,b)上存在零点.上图是用二分法求方程f(x)=0近似解的程序框图,判断框内可以填写的内容有如下四个选择:
已知图象不间断函数f(x)是区间[a,b]上的单调函数,且在区间(a,b)上存在零点.上图是用二分法求方程f(x)=0近似解的程序框图,判断框内可以填写的内容有如下四个选择: