题目内容
对任意的x∈[-2，1]时，不等式x2+2x-a≤0恒成立，则实数a的取值范围是（ ）
| A、（-∞，0] |
| B、（-∞，3] |
| C、[0，+∞） |
| D、[3，+∞） |
考点：函数恒成立问题
专题：函数的性质及应用,不等式的解法及应用
分析：把不等式x2+2x-a≤0变形，分离参数a后求x2+2x在x∈[-2，1]上的最大值，则实数a的取值范围可求．
解答：
解：由x2+2x-a≤0，得a≥x2+2x=（x+1）2-1，
当x∈[-2，1]时，（x+1）2-1的最大值为（1+1）2-1=3．
∴若对任意的x∈[-2，1]时不等式x2+2x-a≤0恒成立，
则实数a的取值范围是[3，+∞）．
故选：D．
当x∈[-2，1]时，（x+1）2-1的最大值为（1+1）2-1=3．
∴若对任意的x∈[-2，1]时不等式x2+2x-a≤0恒成立，
则实数a的取值范围是[3，+∞）．
故选：D．
点评：本题考查了函数恒成立问题，考查了分离变量法求参数的取值范围，训练了二次函数最值的求法，是基础题．
练习册系列答案
相关题目
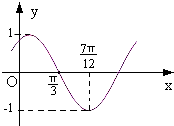已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜| π |
| 2 |
A、ω=1，φ=
| ||
B、ω=2，φ=
| ||
C、ω=1，φ=
| ||
D、ω=2，φ=
|
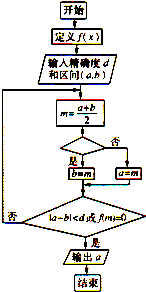已知图象不间断函数f（x）是区间[a，b]上的单调函数，且在区间（a，b）上存在零点．上图是用二分法求方程f（x）=0近似解的程序框图，判断框内可以填写的内容有如下四个选择：①f（a）f（m）＜0，
②f（a）f（m）＞0，
③f（b）f（m）＜0，
④f（b）f（m）＞0，
其中能够正确求出近似解的是（ ）
| A、①④ | B、②③ | C、①③ | D、②④ |
已知直线AB外的任一点O，下列条件中能确定点C与点A、B一定共线的是（ ）
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|