题目内容
9.已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1的左、右顶点分别为A、B,点M为C上不同于A、B的任意一点,则直线MA、MB的斜率之积为( )| A. | $\frac{1}{4}$ | B. | -4 | C. | -$\frac{1}{4}$ | D. | 4 |
分析 求得A和B点坐标,求得直线MA和MB的斜率,由M在椭圆上,x02=4-4y02,即可求得k1•k2=$\frac{{y}_{0}}{{x}_{0}+2}$•$\frac{{y}_{0}}{{x}_{0}-2}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-4}$=-$\frac{1}{4}$.
解答 解:由题意得,椭圆C:$\frac{{x}^{2}}{4}$+y2=1焦点在x轴上,a=2,b=1,
设M(x0,y0)(y0≠0),A(-2,0),B(2,0),
直线MA的斜率k1=$\frac{{y}_{0}}{{x}_{0}+2}$,MB的斜率k2=$\frac{{y}_{0}}{{x}_{0}-2}$,
又点M在椭圆上,
∴$\frac{{x}_{0}^{2}}{4}+{y}_{0}^{2}=1$(y0≠0),x02=4-4y02,
∴k1•k2=$\frac{{y}_{0}}{{x}_{0}+2}$•$\frac{{y}_{0}}{{x}_{0}-2}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-4}$=-$\frac{1}{4}$,
直线MA、MB的斜率之积-$\frac{1}{4}$,
故选C.
点评 本题考查椭圆的标准方程,以及椭圆的简单性质的应用,直线的斜率公式的应用,考查计算能力,属于基础题.

练习册系列答案
相关题目
19.已知集合A={x|x>-1},则下列选项正确的是( )
| A. | 0⊆A | B. | {0}⊆A | C. | ∅∈A | D. | {0}∈A |
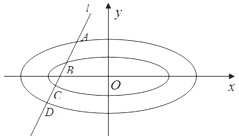 已知椭圆C1,C2均为中心在原点,焦点在x轴上的椭圆,离心率均为$\frac{{\sqrt{2}}}{2}$,其中C1的焦点坐标分别为(-1,0),(1,0),C2的左右顶点坐标为(-2,0),(2,0).
已知椭圆C1,C2均为中心在原点,焦点在x轴上的椭圆,离心率均为$\frac{{\sqrt{2}}}{2}$,其中C1的焦点坐标分别为(-1,0),(1,0),C2的左右顶点坐标为(-2,0),(2,0).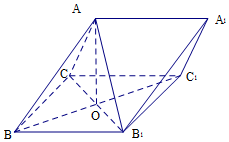 如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C 为菱形,B1C与BC1交于点O,AO⊥平面BB1C1C
如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C 为菱形,B1C与BC1交于点O,AO⊥平面BB1C1C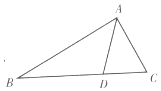 如图,在△ABC中,$AB=2AC,cosB=\frac{{2\sqrt{5}}}{5}$,点D在线段BC上.
如图,在△ABC中,$AB=2AC,cosB=\frac{{2\sqrt{5}}}{5}$,点D在线段BC上.