题目内容
已知f(x)=lg(-x2+4x).
(1)求函数f(x)的定义域、值域;
(2)写出函数f(x)的单调区间.
(1)求函数f(x)的定义域、值域;
(2)写出函数f(x)的单调区间.
考点:复合函数的单调性
专题:函数的性质及应用
分析:(1)根据函数成立的条件即可求函数f(x)的定义域、值域;
(2)根据复合函数单调性之间的关系即可求出函数的单调区间.
(2)根据复合函数单调性之间的关系即可求出函数的单调区间.
解答:
解:(1)要使函数有意义,则-x2+4x>0,即x2-4x<0,解得0<x<4,即函数f(x)的定义域为(0,4)、
设t=-x2+4x,则t=-x2+4x=-(x-2)2+4∈(0,4],
则f(x)=lg(-x2+4x)≤lg4,
即函数的值域为(-∞,lg4];
(2)∵t=-x2+4x=-(x-2)2+4,
∴当x∈(0,2]时,函数t=-x2+4x单调递增,而y=lgt单调递增,即此时函数f(x)单调递增,
当x∈[2,4)时,函数t=-x2+4x单调递减,而y=lgt单调递增,即此时函数f(x)单调递减,
即函数f(x)的单调增区间为(0,2],单调递减区间为[2,4).
设t=-x2+4x,则t=-x2+4x=-(x-2)2+4∈(0,4],
则f(x)=lg(-x2+4x)≤lg4,
即函数的值域为(-∞,lg4];
(2)∵t=-x2+4x=-(x-2)2+4,
∴当x∈(0,2]时,函数t=-x2+4x单调递增,而y=lgt单调递增,即此时函数f(x)单调递增,
当x∈[2,4)时,函数t=-x2+4x单调递减,而y=lgt单调递增,即此时函数f(x)单调递减,
即函数f(x)的单调增区间为(0,2],单调递减区间为[2,4).
点评:本题主要考查函数的定义域,值域以及函数单调区间的求解,根据复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
已知S=
•(sin
+sin
+sin
+…+sin
),则与S的值最接近的是( )
| π |
| 20000 |
| π |
| 20000 |
| 2π |
| 20000 |
| 3π |
| 20000 |
| 10000π |
| 20000 |
| A、0.99818 |
| B、0.9999 |
| C、1.0001 |
| D、2.0002 |
 设全集U=R,A={x|2x(x-2)<1},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )
设全集U=R,A={x|2x(x-2)<1},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )| A、{x|x≥1} |
| B、{x|x≤1} |
| C、{x|0<x≤1} |
| D、{x|1≤x<2} |
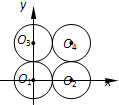 如图,有4个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0),O3(0,2),O4(2,2).记集合M={⊙Oi|i=1,2,3,4}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对”(当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中“有序集合对”(A,B) 的个数是( )
如图,有4个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0),O3(0,2),O4(2,2).记集合M={⊙Oi|i=1,2,3,4}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对”(当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中“有序集合对”(A,B) 的个数是( )