题目内容
10.已知复数z=3+4i,i为虚数单位,$\overline z$是z的共轭复数,则$\frac{i}{\overline{z}}$=( )| A. | $-\frac{4}{5}+\frac{3}{5}i$ | B. | $-\frac{4}{5}-\frac{3}{5}i$ | C. | $-\frac{4}{25}+\frac{3}{25}i$ | D. | $-\frac{4}{25}-\frac{3}{25}i$ |
分析 由z求出$\overline{z}$,代入$\frac{i}{\overline{z}}$,然后利用复数代数形式的乘除运算化简得答案.
解答 解:∵z=3+4i,
∴$\frac{i}{\overline{z}}$=$\frac{i}{3-4i}=\frac{i(3+4i)}{(3-4i)(3+4i)}=-\frac{4}{25}+\frac{3}{25}i$.
故选:C.
点评 本题考查复数代数形式的乘除运算,考查了共轭复数的概念,是基础题.

练习册系列答案
相关题目
18.复数z=$\frac{2-i}{1+i}$(其中i是虚数单位)的虚部为( )
| A. | $-\frac{3}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{3}{2}$ | D. | $\frac{1}{2}$ |
5.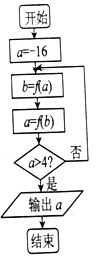 在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )
在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )
 在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )
在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )| A. | 16 | B. | 8 | C. | 216 | D. | 28 |
15.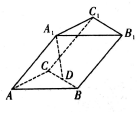 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
2.4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机有放回的抽取2张,则取出的2张卡片上的数字之差的绝对值为奇数的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
19.复数z满足z=$\overline{z}$+$\frac{1+i}{1-i}$,其中$\overline{z}$为z的共轭复数,则z的虚部是( )
| A. | 1 | B. | i | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$i |
20.定义$\frac{n}{{p}_{1}+{p}_{2}+…+{p}_{n}}$为n个正数p1,p2,…,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}+1}{4}$,则$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+$\frac{1}{{b}_{3}{b}_{4}}$+…+$\frac{1}{{b}_{2015}{b}_{2016}}$=( )
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{1}{2015}$ |
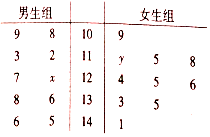 在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图:
在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图: