题目内容
四面体A-BCD中,AB=CD=4,BC=AC=AD=BD=5,则四面体外接球的表面积为 .
考点:球的体积和表面积
专题:球
分析:分别取AB,CD的中点E,F,连接相应的线段,由条件可知,球心G在EF上,可以证明G为EF中点,求出球的半径,然后求出球的表面积.解答:点评:
解答:
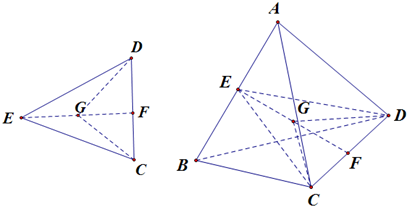 解:分别取AB,CD的中点E,F,连接相应的线段CE,ED,EF,由条件,AB=CD=4,BC=AC=AD=BD=5,可知,△ABC与△ADB,都是等腰三角形,
解:分别取AB,CD的中点E,F,连接相应的线段CE,ED,EF,由条件,AB=CD=4,BC=AC=AD=BD=5,可知,△ABC与△ADB,都是等腰三角形,
AB⊥平面ECD,∴AB⊥EF,同理CD⊥EF,∴EF是AB与CD的公垂线,球心G在EF上,可以证明G为EF中点,(△AGB≌△CGD)
DE=
=
,DF=2,EF=
=
,
∴GF=
=
,
球半径DG=
=
=
,
∴外接球的表面积为4πDG2=4π×
=33π,
故答案为:33π.
 解:分别取AB,CD的中点E,F,连接相应的线段CE,ED,EF,由条件,AB=CD=4,BC=AC=AD=BD=5,可知,△ABC与△ADB,都是等腰三角形,
解:分别取AB,CD的中点E,F,连接相应的线段CE,ED,EF,由条件,AB=CD=4,BC=AC=AD=BD=5,可知,△ABC与△ADB,都是等腰三角形,AB⊥平面ECD,∴AB⊥EF,同理CD⊥EF,∴EF是AB与CD的公垂线,球心G在EF上,可以证明G为EF中点,(△AGB≌△CGD)
DE=
| 25-4 |
| 21 |
| 21-4 |
| 17 |
∴GF=
| EF |
| 2 |
| ||
| 2 |
球半径DG=
|
|
| ||
| 2 |
∴外接球的表面积为4πDG2=4π×
| 33 |
| 4 |
故答案为:33π.
点评:本题考查球的内接几何体,球的表面积的求法,考查计算能力.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知i为虚数单位,则复数2i(1+i)的模是( )
| A、4 | ||
B、2
| ||
C、3
| ||
| D、8 |
 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形且∠A1AC=∠DAB=60°,平面AA1C1C⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形且∠A1AC=∠DAB=60°,平面AA1C1C⊥平面ABCD. 如图,正方形ABCD与梯形CDEF所在的平面互相垂直,CD⊥DE,CF∥DE,CD=CF=2,DE=4,G为AE的中点.
如图,正方形ABCD与梯形CDEF所在的平面互相垂直,CD⊥DE,CF∥DE,CD=CF=2,DE=4,G为AE的中点. 如图,已知正方体ABCD-A1B1C1D1,截去三个角A-BDA1,C-BDC1,B1-BA1C1后形成的几何体的体积与原正方体的体积之比值为
如图,已知正方体ABCD-A1B1C1D1,截去三个角A-BDA1,C-BDC1,B1-BA1C1后形成的几何体的体积与原正方体的体积之比值为