题目内容
若曲线x2+y2=9上各点的横坐标保持不变,纵坐标缩短为原来的一半,则所得曲线方程是 .
考点:轨迹方程
专题:综合题,直线与圆
分析:设出纵坐标变化后的点的坐标,得到原来的坐标,代入圆的方程整理后得答案.
解答:
解:设所求曲线上的任意一点为(x,y),则该点对应的圆x2+y2=9上的点为(x,2y),
代入圆x2+y2=9得:x2+4y2=9,
即
+
=1.
故答案为:
+
=1.
代入圆x2+y2=9得:x2+4y2=9,
即
| x2 |
| 9 |
| 4y2 |
| 9 |
故答案为:
| x2 |
| 9 |
| 4y2 |
| 9 |
点评:本题考查了轨迹方程,训练了代入法求曲线方程,是中档题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
设函数f(x)=sin(ωx+
)(ω>0)的最小正周期为π,则f(x)( )
| π |
| 2 |
A、在(0,
| ||||
B、在(
| ||||
C、在(0,
| ||||
D、在(
|
甲、乙、丙、丁、戊五人并排站成一排,如果甲必须站在乙的右边(甲、乙可以不相邻)那么不同的排法共有( )
| A、24种 | B、60种 |
| C、90种 | D、120种 |
 如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2
如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2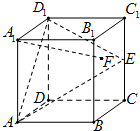 在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值的取值范围是
在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值的取值范围是