题目内容
17．若角θ的终边经过一点A（1，-3），则sinθ=-$\frac{3\sqrt{10}}{10}$；cosθ=$\frac{\sqrt{10}}{10}$；tanθ=-3．分析 根据三角函数的定义，先计算r，再利用正弦余弦正切函数的定义求出．
解答 解：∵x=1，y=-3，
∴r=$\sqrt{10}$，
∴sinθ=$\frac{y}{r}$=$\frac{-3}{\sqrt{10}}$=-$\frac{3\sqrt{10}}{10}$；cosθ=$\frac{x}{r}$=$\frac{1}{\sqrt{10}}$=$\frac{\sqrt{10}}{10}$；tanθ=$\frac{y}{r}$=-3，
故答案为：-$\frac{3\sqrt{10}}{10}$；$\frac{\sqrt{10}}{10}$；-3．
点评 本题考查任意角的三角函数的定义，基本知识的考查．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
7．命题?x∈R，x2-x-1＜0的否定是（ ）
| A． | ?x∈R，x2-x-1≥0 | B． | ?x∈R，x2-x-1＜0 | C． | ?x∈R，x2-x-1＞0 | D． | ?x∈R，x2-x-1≥0 |
12．设数列{an}的前n项和为Sn，且an=2-2Sn，（n∈N*），则数列{an}的通项公式an等于（ ）
| A． | 3n | B． | $\frac{2}{{3}^{n}}$ | C． | $\frac{1}{{3}^{n}}$ | D． | 3n-2 |
6．
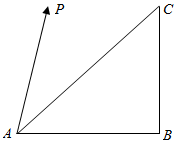等腰直角△ABC的直角顶点为B，两条直角边长都为1，点P为三角形所在平面内的一点，若$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$，且|$\overrightarrow{AP}$|=1，则λ的取值范围为（ ）
等腰直角△ABC的直角顶点为B，两条直角边长都为1，点P为三角形所在平面内的一点，若$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$，且|$\overrightarrow{AP}$|=1，则λ的取值范围为（ ）| A． | [-1，$\sqrt{2}$] | B． | [-$\sqrt{2}$，$\sqrt{2}$] | C． | [-$\sqrt{2}$，1] | D． | [-1，1] |