题目内容
2.已知不等式x2-ax+a-2>0(a>2)的解集为(-∞,x1)∪(x2,+∞),则x1+x2+$\frac{1}{{{x}_{1}x}_{2}}$的最小值为4.分析 由二次不等式的解集和对应方程根的关系以及韦达定理可得x1+x2+$\frac{1}{{{x}_{1}x}_{2}}$=a+$\frac{1}{a-2}$=a-2+$\frac{1}{a-2}$+2,由基本不等式可得.
解答 解:∵不等式x2-ax+a-2>0(a>2)的解集为(-∞,x1)∪(x2,+∞),
∴x1+x2+$\frac{1}{{{x}_{1}x}_{2}}$=a+$\frac{1}{a-2}$=a-2+$\frac{1}{a-2}$+2≥2$\sqrt{(a-2)•\frac{1}{a-2}}$+2=4,
当且仅当a-2=$\frac{1}{a-2}$即a=3时,上式取最小值4,
故答案为:4.
点评 本题考查一元二次不等式的解法,涉及基本不等式求最值,属基础题.

练习册系列答案
相关题目
13.已知集合A={1,2,3,4},B={x|x-1>1},则A∩B=( )
| A. | {1,2} | B. | {2,3} | C. | {3,4} | D. | {2,3,4} |
7.函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(-$\frac{π}{2}$)=( )
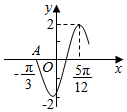
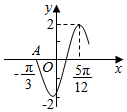
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
12.在中秋节前,小雨的妈妈买来5种水果,4种肉类食品做月饼.要求每种馅只能用两种食材,且水果和肉类不能混合在一起做馅,则小雨妈妈做出水果馅月饼的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{9}$ |