题目内容
5.已知x是等差数列1,4,7,10,…中的某一项,且有1+4+7+10+…+x=590,x是这个等差数列的第几项?求出x的值.分析 根据等差数列的前n项和公式列方程解出n,根据通项公式求出x.
解答 解:设等差数列的公差为d,首项为a1,x是数列的第n项,
则a1=1,d=4-1=3,x=an=1+3(n-1)=3n-2.
∴$\frac{1+3n-2}{2}×n=590$,解得n=20,
∴x=3×20-2=58.
点评 本题考查了等差数列的通项公式,前n项和公式,属于基础题.

练习册系列答案
相关题目
13.已知集合A={1,2,3,4},B={x|x-1>1},则A∩B=( )
| A. | {1,2} | B. | {2,3} | C. | {3,4} | D. | {2,3,4} |
20.函数y=$\frac{2x-1}{\sqrt{3x+5}}$的定义域为( )
| A. | {x|x≥-$\frac{5}{3}$} | B. | {x|x≥-$\frac{5}{3}$且x≠$\frac{1}{2}$} | C. | {x|x>-$\frac{5}{3}$} | D. | {x|x≤-$\frac{5}{3}$} |
15.执行如图所示的程序框图,若输入n=10,则输出的S=( )
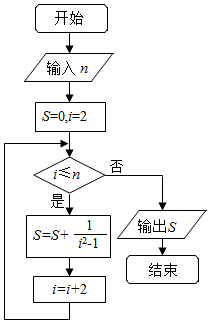

| A. | $\frac{5}{11}$ | B. | $\frac{20}{21}$ | C. | $\frac{10}{21}$ | D. | $\frac{10}{11}$ |