题目内容
f(x)=|x|+|x+1|的最小值为m
(Ⅰ)求m的值;
(Ⅱ)x,y,z∈R,且2x+3y+3z=m求x2+y2+z2的最小值.
(Ⅰ)求m的值;
(Ⅱ)x,y,z∈R,且2x+3y+3z=m求x2+y2+z2的最小值.
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用,不等式
分析:(Ⅰ)利用绝对值不等式f(x)=|x|+|x+1|≥|-x+x+1|=1,结合已知即可求得m的值;
(Ⅱ)利用柯西不等式:(2x+3y+3z)2≤(22+32+32)(x2+y2+z2)即可求得x2+y2+z2的最小值.
(Ⅱ)利用柯西不等式:(2x+3y+3z)2≤(22+32+32)(x2+y2+z2)即可求得x2+y2+z2的最小值.
解答:
解:(Ⅰ)∵f(x)≥|-x+x+1|=1,
∴f(x)的最小值为1,即m=1…(3分)
(Ⅱ)由柯西不等式得:(2x+3y+3z)2≤(22+32+32)(x2+y2+z2).
∵2x+3y+3z=1,
∴x2+y2+z2≥
,当且仅当
=
=
,即x=
,y=z=
时,等号成立,
∴x2+y2+z2的最小值为
.…(7分)
∴f(x)的最小值为1,即m=1…(3分)
(Ⅱ)由柯西不等式得:(2x+3y+3z)2≤(22+32+32)(x2+y2+z2).
∵2x+3y+3z=1,
∴x2+y2+z2≥
| 1 |
| 22 |
| x |
| 2 |
| y |
| 3 |
| z |
| 3 |
| 1 |
| 11 |
| 3 |
| 22 |
∴x2+y2+z2的最小值为
| 1 |
| 22 |
点评:本题主要考查绝对值不等式的解法与柯西不等式等基础知识,考查推理论证能力、运算求解能力.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
已知θ为实数,若复数z=sin2θ-1+i(
cosθ-1)是纯虚数,则z的虚部为( )
| 2 |
| A、2 | B、0 | C、-2 | D、-2i |
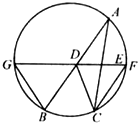 如图,D,E分别为△ABC边AB,AC的中点,直线DE交于△ABC的外接圆于F,G两点,若BC=2EF,证明:
如图,D,E分别为△ABC边AB,AC的中点,直线DE交于△ABC的外接圆于F,G两点,若BC=2EF,证明: