题目内容
某技术部门对工程师进行达标定级考核,需要经过两轮测试,每轮测试的成绩在9.5分及以上的定位该轮测试通过,只有通过第一轮测试的人员才能进行第二轮测试,两轮测试的过程相互独立,并规定
①两轮测试均通过的一定为一级工程师;
②仅通过第一轮测试,而第二轮测试没通过的定为二级工程师;
③第一轮测试没通过的不予定级.
已知甲、乙、丙三位工程师通过第一轮测试的概率分别为
,
,
;通过第二轮测试的概率均为
.
(1)求经过本次考核,甲被定位以及工程师,乙被定位二级工程师的概率;
(2)求经过本次考核,甲、乙、丙三位工程师中恰有两位被定位以及工程师的概率;
(3)设甲、乙、丙三位工程师中被定位一级工程师的人数为随机变量X,求X的分布列和数学期望.
①两轮测试均通过的一定为一级工程师;
②仅通过第一轮测试,而第二轮测试没通过的定为二级工程师;
③第一轮测试没通过的不予定级.
已知甲、乙、丙三位工程师通过第一轮测试的概率分别为
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
(1)求经过本次考核,甲被定位以及工程师,乙被定位二级工程师的概率;
(2)求经过本次考核,甲、乙、丙三位工程师中恰有两位被定位以及工程师的概率;
(3)设甲、乙、丙三位工程师中被定位一级工程师的人数为随机变量X,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:二项式定理
分析:(1)利用相互独立事件同时发生的概率公式计算即可;
(2l利用独立事件的概率乘法公式计算即可
(3)被定位一级工程师的人数为随机变量X取值分别为0,1,2,3,求出相应的概率,即可求数学期望EX.
(2l利用独立事件的概率乘法公式计算即可
(3)被定位一级工程师的人数为随机变量X取值分别为0,1,2,3,求出相应的概率,即可求数学期望EX.
解答:
解:(1)甲被定位一级工程师概率是
×
=
,乙被定位二级工程师的概率
×(1-
)=
,甲被定位一级工程师,乙被定位二级工程师的概率是
×
=
.
(2)甲被定位一级工程师概率是
,乙丙各自被定为一级工程师的概率都是
,甲和乙被定为一级:
×
×(1-
)=
,
甲和丙被定为一级
×(1-
)×
=
,乙丙被定为一级:(1-
)×
×
=
,则有两人被定为一级工程师的概率为:
+
+
=
(3)甲乙丙都没有定为一级的概率是(1-
)×(1-
)×(1-
)=
,有一个被定为一级工程师的概率是
,三人都被定为一级工程师的概率是
,
所以X的分布列是:
数学期望是EX=0×
+1×
+2×
+3×
=
.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 18 |
(2)甲被定位一级工程师概率是
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 27 |
甲和丙被定为一级
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 27 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 54 |
| 1 |
| 27 |
| 1 |
| 27 |
| 5 |
| 54 |
| 1 |
| 6 |
(3)甲乙丙都没有定为一级的概率是(1-
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 10 |
| 27 |
| 4 |
| 9 |
| 1 |
| 54 |
所以X的分布列是:
| x | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 10 |
| 27 |
| 4 |
| 9 |
| 1 |
| 6 |
| 1 |
| 54 |
| 5 |
| 6 |
点评:本题考查了互斥事件、对立事件的概率,考查了独立事件的概率乘法公式,考查了系数分析、解决问题的能力.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
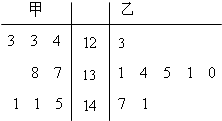 为了解某校高一学生的中考数学成绩,分别从甲乙两班随机各抽取8名学生的中考数学成绩,获得如图所示的茎叶图.
为了解某校高一学生的中考数学成绩,分别从甲乙两班随机各抽取8名学生的中考数学成绩,获得如图所示的茎叶图.
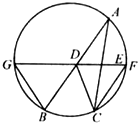 如图,D,E分别为△ABC边AB,AC的中点,直线DE交于△ABC的外接圆于F,G两点,若BC=2EF,证明:
如图,D,E分别为△ABC边AB,AC的中点,直线DE交于△ABC的外接圆于F,G两点,若BC=2EF,证明: