Question

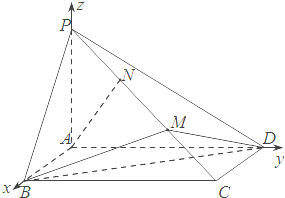己知四棱锥P-ABCD，其中底面ABCD为矩形侧棱PA⊥底面ABCD，其中BC=2，AB=2PA=6，M，N为侧棱PC上的两个三等分点，如图所示：
（Ⅰ）求证：AN∥平面MBD；
（Ⅱ）求二面角B-PC-A的余弦值．

Answer 1

考点：用空间向量求平面间的夹角,直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（Ⅰ）连结AC交BD于O，连结OM，利用直线与平面平行的判定定理证明：AN∥平面MBD；
（Ⅱ）设平面BCP的法向量为

m

=(x，y，z)，利用向量的垂直关系，求出法向量，同样求出平面PAC法向量

n

=(x1，y1，z1)，利用空间向量的数量积，直接求解二面角B-PC-A的余弦值．

解答： （Ⅰ）证明：连结AC交BD于O，连结OM，
∵底面ABCD为矩形，∴O为AC中点，∵M、N为侧棱PC的三等份点，∴MN=CM，
∴OM∥AN，∵OM?平面MBD，AN?平面MBD，∴AN∥平面MBD  （4分）．
（Ⅱ）易知△ABP为等腰直角三角形，所以BP为外接圆的直径，所以PB=3

2

，PA=3
如图所示，以A为原点，建立空间直角坐标系A-xyz，
则A（0，0，0），B（3，0，0），C（3，6，0），D（0，6，0），P（0，0，3），M（2，4，1），N（1，2，2），
设平面BCP的法向量为

m

=(x，y，z)，∵

BP

=(-3，0，3)，

BC

=(0，6，0)，
并且m⊥

BP

，m⊥

BC

，∴

-3x+3z=0 6y=0

，令x=1，得y=0，z=1，
∴平面MBD的一个法向量为

m

=(1，0，1)，（6分）
设平面PAC法向量为

n

=(x1，y1，z1)，
同理可得

n

=(2，-1，0)（8分）
cos＜

m

，

n

＞=

m • n

|m || n |

=

2

2 5

=

10

5

（10分）
由图可知，二面角B-PC-A为锐角，
∴二面角B-PC-A的余弦值为

10

5

．（12分）

点评：本题考查直线与平面平行的判定定理，二面角的平面角的求法，考查空间想象能力以及计算能力．