题目内容
11．函数y=（$\frac{1}{2}$）${\;}^{2{x}^{2}-3x+1}$的递减区间为（ ）| A． | [$\frac{3}{4}$，+∞） | B． | （-∞，$\frac{3}{4}$] | C． | （-∞，1） | D． | （1，+∞） |
分析 利用二次函数的性质以及指数函数的单调性，结合复合函数的单调性求解即可．
解答 解：函数y=$（\frac{1}{2}）^{x}$是减函数，y=2x2-3x+1，开口向上，x∈[$\frac{3}{4}$，+∞）是二次函数的增区间，
由复合函数的单调性可知：函数y=（$\frac{1}{2}$）${\;}^{2{x}^{2}-3x+1}$的递减区间为：[$\frac{3}{4}$，+∞）．
故选：A．
点评 本题考查复合函数的单调区间的求法，复合函数的单调性的应用，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
2．
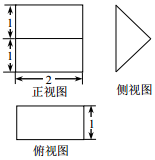《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，已知某“堑堵”的三视图如图所示，则该“堑堵”的表面积为（ ）
《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，已知某“堑堵”的三视图如图所示，则该“堑堵”的表面积为（ ）| A． | 4 | B． | $6+4\sqrt{2}$ | C． | $4+4\sqrt{2}$ | D． | 2 |
19．正实数ab满足$\frac{1}{a}$+$\frac{2}{b}$=1，则（a+2）（b+4）的最小值为（ ）
| A． | 16 | B． | 24 | C． | 32 | D． | 40 |
16．将直线y=2x绕原点逆时针旋转90°，再向右平移1个单位，所得到的直线为（ ）
| A． | $y=-\frac{1}{2}x+\frac{1}{2}$ | B． | $y=-\frac{1}{2}x+1$ | C． | y=2x-2 | D． | $y=\frac{1}{2}x+1$ |
3．下列函数中，既是偶函数又在（-∞，0）内为增函数的是（ ）
| A． | y=（$\frac{1}{2}$）x | B． | y=x-2 | C． | y=x2+1 | D． | y=log3（-x） |
20．已知集合A={x|-1＜x＜3}，B={x|-2＜x＜1，x∈z}，则A∩B=（ ）
| A． | {0} | B． | [-1，1] | C． | {-1，0，1，2} | D． | D=[-2，3] |