题目内容
1.已知$f(x)=\left\{{\begin{array}{l}{4x-{x^2},x<1}\\{{e^x},x≥1}\end{array}}\right.$,若方程f(x)=kx有且仅有一个实数解,则实数k的取值范围为(-∞,e).分析 画出分段函数与y=kx的图象,利用方程f(x)=kx有且仅有一个实数解,判断看的范围即可.
解答 解:$f(x)=\left\{{\begin{array}{l}{4x-{x^2},x<1}\\{{e^x},x≥1}\end{array}}\right.$,若方程f(x)=kx有且仅有一个实数解,
就是分段函数与y=kx的图象只有一个交点,如图: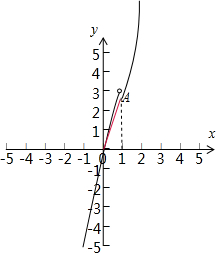
显然k小于OA的斜率时满足题意,y=ex,x≥1,导函数为y′=ex,是增函数,当x=1时函数取得最小值,此时OA的斜率最小,最小值为:e,可得k<e.
故答案为:(-∞,e).
点评 本题考查函数的零点的求法,导数的应用,函数的单调性与导数的关系,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.与α=$\frac{π}{12}$+2kπ(k∈Z)终边相同的角是( )
| A. | 345° | B. | 375° | C. | -$\frac{11}{12}$π | D. | $\frac{23}{12}$π |
12.函数f(x)=$\frac{1}{\sqrt{1-{2}^{x}}}$的定义域是( )
| A. | (-∞,$\frac{1}{2}$) | B. | (-∞,0] | C. | (0,+∞) | D. | (-∞,0) |
9.已知集合A={1,4},B={y|y=log2x,x∈A},则A∪B=( )
| A. | {1,4} | B. | {0,1,4} | C. | {0,2} | D. | {0,1,2,4} |
13.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的焦点到渐近线的距离为2,且双曲线的一条渐近线与直线x-2y+3=0平行,则双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
11.函数y=($\frac{1}{2}$)${\;}^{2{x}^{2}-3x+1}$的递减区间为( )
| A. | [$\frac{3}{4}$,+∞) | B. | (-∞,$\frac{3}{4}$] | C. | (-∞,1) | D. | (1,+∞) |
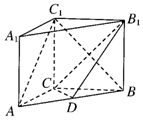 如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.