题目内容
2.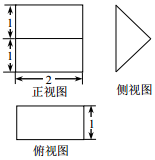 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )| A. | 4 | B. | $6+4\sqrt{2}$ | C. | $4+4\sqrt{2}$ | D. | 2 |
分析 由已知中的三视图可得:该几何体是一个以主视图为底面的三棱柱,代入棱柱表面积公式,可得答案.
解答 解:由已知中的三视图可得:该几何体是一个以主视图为底面的三棱柱,
底面面积为:$\frac{1}{2}$×2×1=1,
底面周长为:2+2×$\sqrt{2}$=2+2$\sqrt{2}$,
故棱柱的表面积S=2×1+2×(2+2$\sqrt{2}$)=6+4$\sqrt{2}$,
故选:B.
点评 本题考查的知识点是棱柱的体积和表面积,棱锥的体积和表面积,简单几何体的三视图,难度基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.函数f(x)=$\frac{1}{\sqrt{1-{2}^{x}}}$的定义域是( )
| A. | (-∞,$\frac{1}{2}$) | B. | (-∞,0] | C. | (0,+∞) | D. | (-∞,0) |
13.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的焦点到渐近线的距离为2,且双曲线的一条渐近线与直线x-2y+3=0平行,则双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
7.已知O为坐标原点,F是双曲线$Γ:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点,A,B分别为Γ的左、右顶点,P为Γ上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E,直线 BM与y轴交于点N,若|OE|=2|ON|,则 Γ的离心率为( )
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
14.两座灯塔A和B与海洋观测站C的距离分别是akm和2akm,灯塔A在观测站C的北偏东20°,灯塔B在观测站C的南偏东40°,则灯塔A与灯塔B之间的距离为( )
| A. | $\sqrt{3}$akm | B. | 2akm | C. | $\sqrt{5}$akm | D. | $\sqrt{7}$akm |
11.函数y=($\frac{1}{2}$)${\;}^{2{x}^{2}-3x+1}$的递减区间为( )
| A. | [$\frac{3}{4}$,+∞) | B. | (-∞,$\frac{3}{4}$] | C. | (-∞,1) | D. | (1,+∞) |
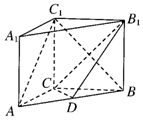 如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.