题目内容
12.下列4个命题中假命题的是①②④(写上对应的程序号)①若p∨q为真命题,p∧q为假命题,则q为假命题
②命题“如果$\sqrt{x-1}$=2,则(x+1)(x-5)=0”的否命题是真命题
③“方程x2+x+m=0有实数根”是“m<$\frac{1}{4}$”的必要不充分条件
④命题p:?x∈R,x+$\frac{1}{x}$<2的否定为¬p:?x∉R,x+$\frac{1}{x}$≥2.
分析 ①,若p∨q为真命题,p∧q为假命题,则q、p有一个为假命题,一个为真;
②,$\sqrt{x-1}$≠2时,(x+1)(x-5)=0可能成立;
③,方程x2+x+m=0有实数根⇒△=1-4m≥0⇒是m≤$\frac{1}{4}$;
④,命题的否定只否定结论,不否定条件,
解答 解:对于①,若p∨q为真命题,p∧q为假命题,则q、p有一个为假命题,一个为真,故错;
对于②,$\sqrt{x-1}$≠2时,(x+1)(x-5)=0可能成立,故错;
对于③,方程x2+x+m=0有实数根⇒△=1-4m≥0⇒是m≤$\frac{1}{4}$ 故正确;
对于,④命题p:?x∈R,x+$\frac{1}{x}$<2的否定为¬p:?x∈R,x+$\frac{1}{x}$≥2,故错.
故答案为:①②④
点评 本题考查了命题真假的判定,属于基础题.

练习册系列答案
相关题目
17.已知sin(α+$\frac{π}{3}$)=sinα,则tanα=( )
| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
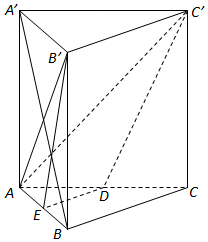 如图所示,直三棱柱ABC-A′B′C中,∠ABC=90°,AB=BC=BB′=2,D为底棱AC的中点.
如图所示,直三棱柱ABC-A′B′C中,∠ABC=90°,AB=BC=BB′=2,D为底棱AC的中点.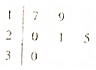 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.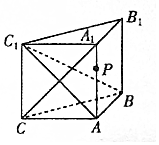 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.