题目内容
14．曲线y=$\sqrt{x}$与直线y=2x-1及x轴所围成的封闭图形的面积为（ ）| A． | $\frac{5}{12}$ | B． | $\frac{11}{12}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{2}$ |
分析 根据定积分的几何意义，先求出积分的上下限，即可求出所围成的图形的面积．
解答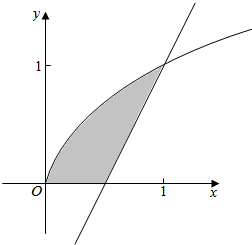 
解：联立曲线y=$\sqrt{x}$与直线y=2x-1构成方程组$\left\{\begin{array}{l}{y=\sqrt{x}}\\{y=2x-1}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$，
联立直线y=2x-1，y=0构成方程组，解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=0}\end{array}\right.$．
∴曲线y=$\sqrt{x}$与直线y=2x-1及x轴所围成的封闭图形的面积：
S=${∫}_{0}^{1}\sqrt{x}dx-$${∫}_{\frac{1}{2}}^{1}（2x-1）dx$=$\frac{2}{3}{x}^{\frac{3}{2}}$${|}_{0}^{1}$$-（{x}^{2}-x）{|}_{\frac{1}{2}}^{1}$=$\frac{2}{3}$+$\frac{1}{4}-\frac{1}{2}$=$\frac{5}{12}$．
故选：A．
点评 本题考查了定积分的几何意义，关键是求出积分的上下限，属于基础题．
练习册系列答案
相关题目
5．若函数f（x）=cos2x+asinx在区间（$\frac{π}{6}$，$\frac{π}{2}$）是减函数，则实数a∈（ ）
| A． | （-∞，2） | B． | （-∞，2] | C． | （4，+∞） | D． | [4，+∞） |
2．设向量$\overrightarrow{a}$=（1，2），|$\overrightarrow{b}$|=2$\sqrt{5}$，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°则$\overrightarrow{a}$•$\overrightarrow{b}$的值为（ ）
| A． | $\sqrt{5}$ | B． | 5 | C． | 5$\sqrt{5}$ | D． | 10 |
9．
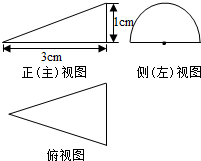一个几何体的三视图及其尺寸如图所示，其中正（主）视图是直角三角形，侧（左）视图是半圆，俯视图是等腰三角形，则这个几何体的表面积是（ ）
一个几何体的三视图及其尺寸如图所示，其中正（主）视图是直角三角形，侧（左）视图是半圆，俯视图是等腰三角形，则这个几何体的表面积是（ ）| A． | $\frac{（\sqrt{10}+1）π}{2}$cm2 | B． | （$\frac{（\sqrt{10}+1）π}{2}$+3）cm2 | C． | （$\frac{π}{2}$+3）cm2 | D． | （$\frac{\sqrt{10}π}{2}$+3）cm2 |
19．考取驾照是一个非常严格的过程，有的人并不能一次性通过，需要进行补考，现在有一张某驾校学员第一次考试结果汇总表：
（1）完成列联表
（2）根据列联表判断性别与考试成绩是否有关系，如果有关系求出精确地可信度，没关系请说明理由．
| 成绩 性别 | 合格 | 不合格 | 合计 |
| 男性 | 45 | 10 | |
| 女性 | 30 | ||
| 合计 | 105 |
（2）根据列联表判断性别与考试成绩是否有关系，如果有关系求出精确地可信度，没关系请说明理由．
6．在长方体ABCD-A′B′C′D′中，$B{B^'}=\sqrt{3}$，B′C′=1，则AA′与BC′所成的角是（ ）
| A． | 90° | B． | 45° | C． | 60° | D． | 30° |