题目内容

18．一个几何体的三视图如图所示，其中正视图是正三角形，则几何体的外接球的表面积为$\frac{64π}{3}$．

分析 根据题意得到该几何体有一个侧面PAC垂直于底面，高为2$\sqrt{3}$，底面是一个等腰直角三角形的三棱锥，如图所示，这个几何体的外接球的球心O在高线PD上，且是等边三角形PAC的中心，求出外接球的半径，即可确定出表面积．

解答 解：由已知中正视图是一个正三角形，侧视图和俯视图均为三角形，
可得该几何体是有一个侧面PAC垂直于底面，高为2$\sqrt{3}$，底面是一个等腰直角三角形的三棱锥，如图所示，
∴这个几何体的外接球的球心O在高线PD上，且是等边三角形PAC的中心，
∴这个几何体的外接球的半径R=$\frac{2}{3}$PD=$\frac{4\sqrt{3}}{3}$，
则几何体的外接球的表面积为4πR2=$\frac{64π}{3}$．
故答案为：$\frac{64π}{3}$

点评 此题考查了由三视图求面积、体积，根据三视图正确画出几何体是解本题的关键．

练习册系列答案
相关题目
10．已知点A（x1，f（x1）），B（x2，f（x2））是函数f（x）=2sin（ωx+φ）（ω＞0．-$\frac{π}{2}$＜φ＜0）图象上的任意两点，且角φ的终边经过点P（1，-$\sqrt{3}$），若|f（x1）-f（x2）|=4，|x1-x2|的最小值为$\frac{π}{3}$．
（1）求函数f（x）的解析式；
（2）将y=f（x）的图象向左平移$\frac{π}{6}$个单位，再将得到的图象的横坐标变为原来的2倍（纵坐标不变）后得到的y=g（x）的图象，求函数y=g（x）的对称中心坐标；
（3）当x∈[0，$\frac{π}{6}$]，不等式mf（x）+2m≥f（x）恒成立，求实数m的取值范围．
9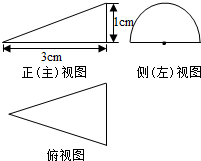．一个几何体的三视图及其尺寸如图所示，其中正（主）视图是直角三角形，侧（左）视图是半圆，俯视图是等腰三角形，则这个几何体的表面积是（　　）
A．$\frac{（\sqrt{10}+1）π}{2}$cm2B．（$\frac{（\sqrt{10}+1）π}{2}$+3）cm2C．（$\frac{π}{2}$+3）cm2D．（$\frac{\sqrt{10}π}{2}$+3）cm2
6．在长方体ABCD-A′B′C′D′中，$B{B^'}=\sqrt{3}$，B′C′=1，则AA′与BC′所成的角是（　　）
A．90°B．45°C．60°D．30°
13．已知函数f（x）=|x-a|，不等式f（x）≤3的解集为[-1，5]．
（Ⅰ）求实数a的值；
（Ⅱ）若f（x）+f（x+5）≥m对一切实数x恒成立，求实数m的取值范围．
3．已知两点F1（-$\sqrt{2}$，0），F2（$\sqrt{2}$，0），满足条件|PF1|-|PF2|=2的动点P的轨迹是曲线E，直线l：y=kx-1与曲线E交于不同两点A、B：
（Ⅰ）求k的取值范围；   
（Ⅱ）若|AB|=2$\sqrt{5}$，求直线l的方程．
10．计算：
（1）2log32-log3$\frac{32}{9}$+log38-5${\;}^{lo{g}_{5}3}$；
（2）sin810°+tan765°+sin1110°+cos（-660°）．
7．函数f（x）=sinπx+cosπx+|sinπx-cosπx|对任意x∈R有f（x1）≤f（x）≤f（x2）成立，则|x2-x1|的最小值为$\frac{3}{4}$．
8．已知a＞b，则下列不等式中恒成立的是（　　）
A．lna＞lnbB．$\frac{1}{a}＜\frac{1}{b}$C．a2＞abD．a2+b2＞2ab

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网