题目内容
16.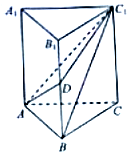 如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.
如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.
分析 将直三棱柱ABC-A1B1C1展开成矩形ACC1A1,如图,连结AC1,交BB1于D,此时AD+DC1最小,当AD+DC1最小时,BD=1,此时三棱锥D-ABC1的体积:${V}_{D-AB{C}_{1}}$=${V}_{{C}_{1}-ABD}$,由此能求出结果.
解答 解: 将直三棱柱ABC-A1B1C1展开成矩形ACC1A1,如图,
将直三棱柱ABC-A1B1C1展开成矩形ACC1A1,如图,
连结AC1,交BB1于D,此时AD+DC1最小,
∵AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,
∴当AD+DC1最小时,BD=1,
此时三棱锥D-ABC1的体积:
${V}_{D-AB{C}_{1}}$=${V}_{{C}_{1}-ABD}$=$\frac{1}{3}×{S}_{△ABD}×{B}_{1}{C}_{1}$
=$\frac{1}{3}×\frac{1}{2}×AB×BD×{B}_{1}{C}_{1}$
=$\frac{1}{3}×\frac{1}{2}×1×1×2$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查几何体的体积的求法,考查空间中线线、线面、面面的位置关系等基础知识,考查推理论证能力、运算求解能力、空间思维能力,考查数数结合思想、函数与方程思想、化归与转化思想,是中档题.

练习册系列答案
相关题目
7.已知F1,F2是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q为线段PF2的中点,则$\frac{{{a^2}+{e^2}}}{b}$(其中e为椭圆C的离心率)的最小值为( )
| A. | $\sqrt{6}$ | B. | $\frac{{3\sqrt{6}}}{4}$ | C. | $\sqrt{5}$ | D. | $\frac{{3\sqrt{5}}}{4}$ |
5.漳州水仙鳞茎硕大,箭多花繁,色美香郁,素雅娟丽,有“天下水仙数漳州”之美誉.现某水仙花雕刻师受雇每天雕刻250粒水仙花,雕刻师每雕刻一粒可赚1.2元,如果雕刻师当天超额完成任务,则超出的部分每粒赚1.7元;如果当天未能按量完成任务,则按实际完成的雕刻量领取当天工资.
(I)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
以10天记录的各雕刻量的频率作为各雕刻量发生的概率.
(ⅰ)求该雕刻师这10天的平均收入;
(ⅱ)求该雕刻师当天收入不低于300元的概率.
(I)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
| 雕刻量n | 210 | 230 | 250 | 270 | 300 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
(ⅰ)求该雕刻师这10天的平均收入;
(ⅱ)求该雕刻师当天收入不低于300元的概率.
20.已知复数z满足$\frac{z}{1+i}=|{2-i}|$,则z的共轭复数对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |

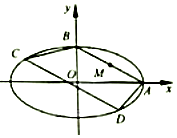 如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..
如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..