题目内容
16.若a>0,b>0,4a+b=ab.(Ⅰ)求a+b的最小值;
(Ⅱ)当a+b取得最小值时,a,b的值满足不等式|x-a|+|x-b|≥t2-2t对任意的x∈R恒成立,求t的取值范围.
分析 (Ⅰ)利用“1”的代换,结合基本不等式,即可求a+b的最小值;
(Ⅱ)利用绝对值不等式|x-a|+|x-b|≥|a-b|=3,因为满足不等式|x-a|+|x-b|≥t2-2t对任意的x∈R恒成立,所以3≥t2-2t,即可求t的取值范围.
解答 解:(Ⅰ)因为4a+b=ab,∴$\frac{4}{b}+\frac{1}{a}$=1,
所以a+b=(a+b)($\frac{4}{b}+\frac{1}{a}$)=5+$\frac{4a}{b}$+$\frac{b}{a}$≥5+4=9,
当且仅当$\frac{4a}{b}$=$\frac{b}{a}$时,即b=2a时,a+b有最小值9,由4a+b=ab,可求得此时a=3,b=6;
(Ⅱ)|x-a|+|x-b|≥|a-b|=3,因为满足不等式|x-a|+|x-b|≥t2-2t对任意的x∈R恒成立,所以3≥t2-2t,解得t∈[-1,3].
点评 本题考查基本不等式的运用,考查绝对值不等式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知数列{an}为等比数列,且a1a13+2a72=5π,则cos(a2a12)的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
11.治理大气污染刻不容缓,根据我国分布的《环境空气质量数(AQI)技术规定》:空气质量指数划分阶为0~50、51~100、101~150、151~200、201~300和大于300六级,对应于空气质量指数的六个级别,指数越大,级别越高,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数小于150时,可以户外运动;空气质量指数151及以上,不适合进行旅游等户外活动,以下是某市2016年12月中旬的空气质量指数情况:
(1)求12月中旬市民不适合进行户外活动的概率;
(2)一外地游客在12月中旬来该市旅游,想连续游玩两天,求适合旅游的概率.
| 时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
| AQI | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
(2)一外地游客在12月中旬来该市旅游,想连续游玩两天,求适合旅游的概率.
8.“2a>2b>1”是“$\root{3}{a}$>$\root{3}{b}$”的( )条件.
| A. | 充要 | B. | 必要不充分 | ||
| C. | 充分不必要 | D. | 既不充分也不必要 |
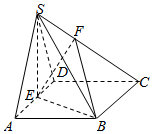 已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\frac{SF}{SC}$=λ,SA∥平面BEF.
已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\frac{SF}{SC}$=λ,SA∥平面BEF.